<< Home
<< andere Sonnenuhr-Beiträge
↓↓ Ende
Ein bemerkenswerter Zusammenhang zwischen Ellipse und Kreis
Vorschlag für ein Sonnenuhren-Zifferblatt
siehe auch: Gerd Ehrhardt: Sonnenuhren, Abschn.: "Zifferblattform für gleiche Flächen in gleichen Zeiten"Der Zusammenhang zwischen Kreis und Ellipse ist ein rein geometrischer: Beide sind Kegelschnitte der der nicht ausgearteten Form. Sie sind geschlossene Linien, und der Kreis ist lediglich ein Sonderfall der Ellipse. Umgekehrt lässt sich eine Ellipse als Allgemeinfall des Kreises beschreiben, was von einem in gleiche Sektoren unterteilten Kreis zu einer in gleiche Sektoren unterteilten Ellipse führt, die beispielsweise in der o.g. Arbeit behandelt wird.
Zwei Beschreibungen:- Eine Ellipse, die in vom Mittelpunkt ausgehenende Sektoren unterteilt ist, entsteht durch schiefe orthogonale Projektion eines Kreises, der in vom Mittelpunkt ausgehenende Sektoren unterteilt ist.
- Die Ellipse samt Sektorengrenzen entsteht auch als Schnittbild beim schrägen Schneiden eines Hohlzylinders (Zylinder als Spezialform des Kegels), in in dessen Achse sich ein Ebenenbüschel befindet.
Beobachtungen in der Physik zeigen oft geometrische Zusammenhänge. Sie sind eine Anwendung der Mathematik. Für die Erklärung der Mathematik sind sie hilfreich, aber nicht erforderlich.
Die im Blog-Artikel erwähnte elliptische Planetenbahn-Ebene als allgemeiner Fall einer Kreisfläche mit von einem Brennpunkt ausgehenden zeitproportionalen Teilflächen ist nicht nur geometrisch sondern auch physikalisch etwas anderes (nicht optische Abbidung sondern beschleunigte Bewegung zwischen zwei Köpern) und scheidet für eine solche Parallele prinzipiell aus.
Für Sonnenuhren-Zifferblätter inkl. der auf ihnen vorkommenden geometrischen Formen gilt, dass sie wie geometrische Zusammenhänge grundsätzlich zeitlos sind. Die Zeitabhängigkeit als physikalische Erscheinung, hier der in ihnen eingefrorenen Tages- Positionen der Sonne am Himmel, fällt aus dem genannten Vergleich heraus.
Die in o.g. Arbeit vorgestellte mathematische Behandlung der Frage, ob die Sektoren auf der Ellipse, die von einem in gleiche Sektoren unterteilten Kreis abgeleitet ist, auch untereinander gleiche große Flächen sind, hat diesen statischen Hintergrund. Sie geht von puren Stundenwinkeln aus, auch wenn Stunde einen Bezug auf Änderung der Zeit hat. Und sie beantwortet die gestellte Frage mit ja, was garnicht überraschend ist. Warum?
Der Kreis ist ein Sonderfall des allgemeinen Falls Ellipse. Dass bei ihm gilt, was für die Ellipse gilt, ist naheliegend, das Umgekehrte ebenso.
Ich habe dennoch ein paar einfache Kontrollrechnungen /-konstruktionen gemacht:
Einfach heißt auch, dass die ausgewählten Sektoren schmal sind (Δα << 1) und somit in guter Näherung als schmale Dreiecke leichter zu berechen sind. Deren Flächen A =Δα· r2 / 2 sind untereinander gleich. Die entsprechenden Kreis-Flächen (Kreis als Ellipsen-Innenkreis) sind bei einer vertikalen Sonnenuhr mit dem Faktor 1 /cosφ kleiner (φ= geograf. Breitenwinkel).
- 18 Uhr: Abb1, blauer Text
Die Dreieckskatheten r ändern sich nicht.
Die Δα als Bogen im Einheitskreis näherungsweise ersetzende Grundseite c wird mit dem Faktor 1 /cos φ größer. Δα wächst im gleichen Maß und somit auch AEll.
Z.B.: φ = 45°: AEll = √2 · AKreis. -
12 Uhr: Abb1, roter Text
Die Dreieckskatheten r werden mit dem Faktor 1 /cosφ größer.
Die Grundseite c ändert sich nicht.
Der Δα -Bogen auf dem Einheitskreis wird aber wegen r = 1 /cosφ > 1 mit dem Faktor cosφ kleiner.
Wegen r2 ist AEll dennoch mit dem Faktor 1 /cosφ größer als AKreis.
Z.B.: φ = 45°: AEll = √2 · AKreis.
Die beiden Sektoren AEll sind gleich groß. Dennoch sei eine dritte, weniger besondere Stelle untersucht: -
15 Uhr: Abb.2
τ =α = 45°
Hier ändern sich sowohl die Dreieckkatheten als auch die Grundseite.
Die Katheten-Enden liegen mit dem Faktor 1/cosφ tiefer und die Katheden sind länger: r = √1,5 = 1,225 (z. B. mit bisherigem φ = 45°).
Die Grundseite c wächst mit demselben Faktor auf c' = 1,225, liegt aber nicht mehr symmetrisch zwischen den Katheten.
Die symmetrische Lage und der etwas kleinere Wert c'' = 1,155 sind nach einer Drehung (19,5°) im Gegenuhrzeigersinn erreicht.
Der Δα -Bogen auf dem Einheitskreis wird aber wegen r=1,225 >1 mit dem Faktor 1/1,225 kleiner: Δα = 0,943. AEll = Δα · r2 = 0,943 · 1,5 = √2 .
Resume: An allen drei Orten der Ellipse sind die Flächen gleich breiter Sektoren - gleich wie bei den Kreissektoren - untereinander gleich groß.
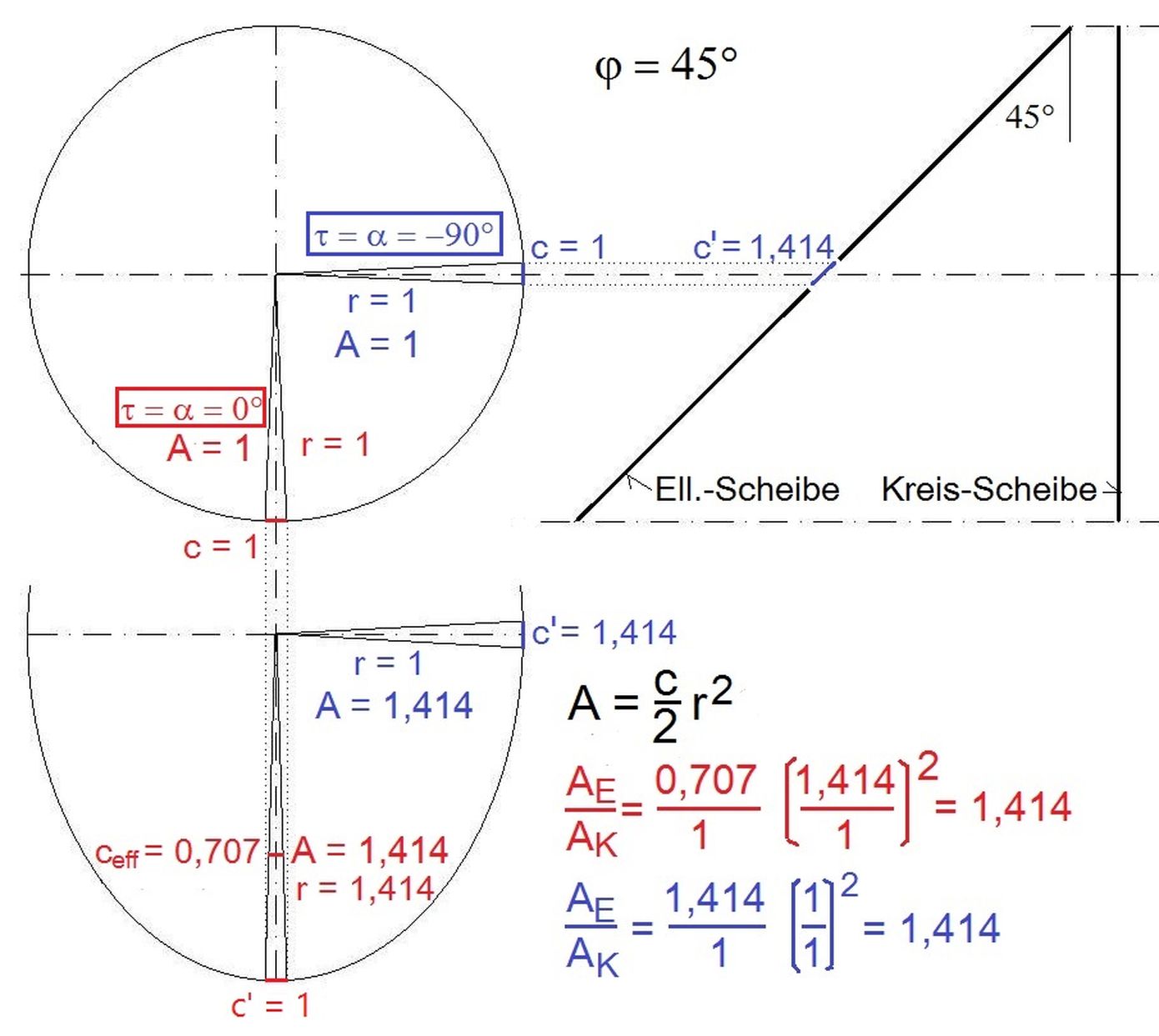 Abb.1 Kontrollzeichnung für 12 Uhr (rot)
Abb.1 Kontrollzeichnung für 12 Uhr (rot) und 06 Uhr (blau; die Verhältnisse sind zwischen 06 Uhr und 18 Uhr spiegelbildlich gleich)
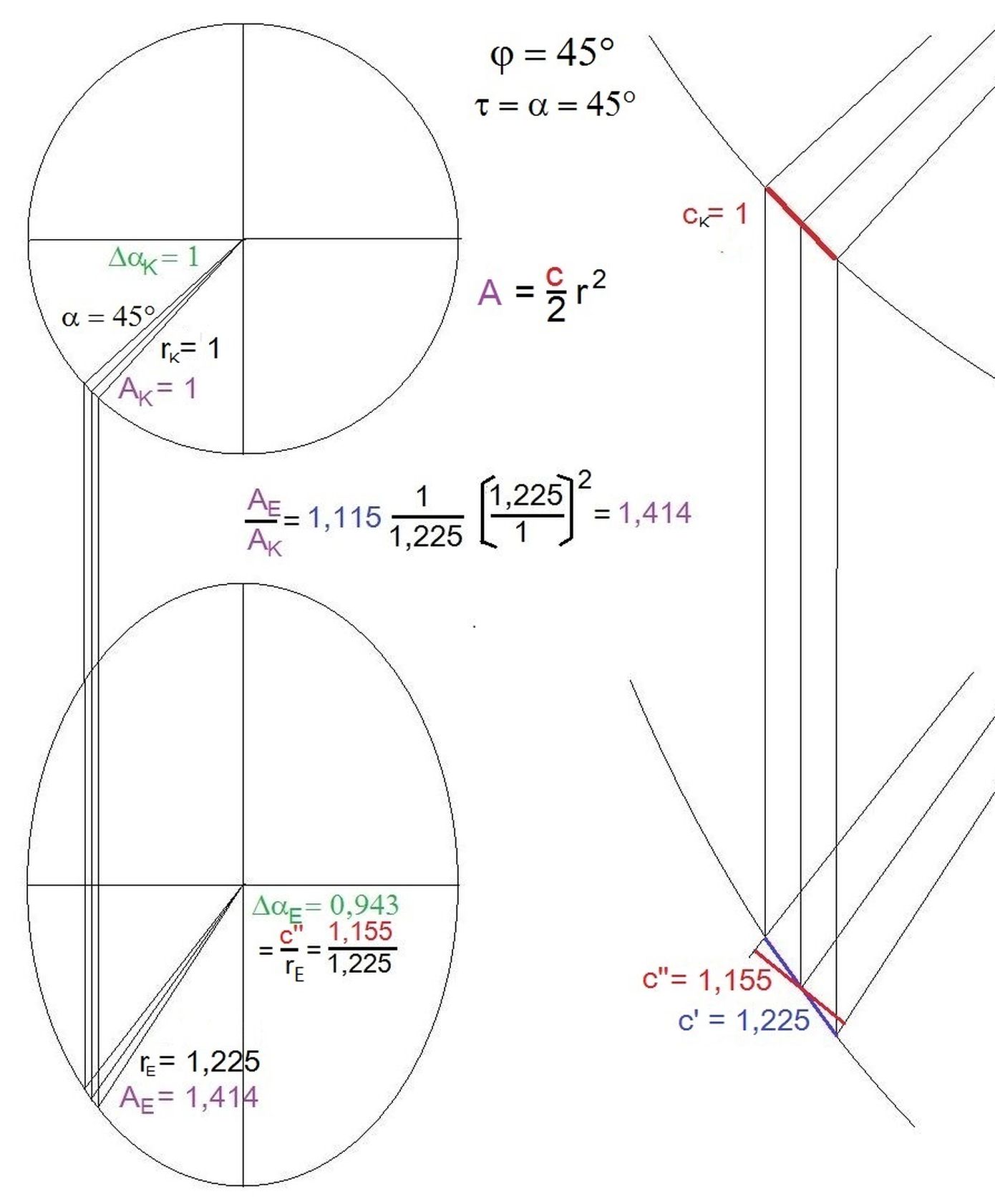 Abb.2 Kontrollzeichnung für 15 Uhr
Abb.2 Kontrollzeichnung für 15 Uhr
In Abb.3 wird ein in der o.g. Arbeit erarbeitetes Sonnenuhren-Zifferblatt in "Form für gleiche Flächen in gleichen Zeiten" gezeigt. Wird dadurch der Formen-Fundus der existierenden Zifferblätter wesentlich bereichert?
Dafür spricht, wenn man es nicht auf einer wie meistens rechteckigen Tafel anbringt, sondern eine Tafel mit geradem oberen Rand und im Übrigen halbellipsenförmig begrenzt ausführt. Man lässt sonst die Stundenlinien, deren Länge für die Zeitmessung nicht, sondern deren Richtung relevant ist, bis zum Tafelrand laufen. Die Tafel ist deshalb breiter als hoch, wobei Bezug darauf genommen ist, dass die Länge des Stabschatten in den Morgen- und Abend- länger als in den Mittagsstunden ist.
Dass die Flächen zwischen den elliptisch begrenzten Stundenlinien alle gleich groß sind, kann dieser Ausführung als "Erfindungshöhe" zugesprochen werden. Nur leider wird das wohl nur von jemanad erkannt, der bereits Kenntnis davon hat, nicht aber von einem "unbedarften" Betrachter.
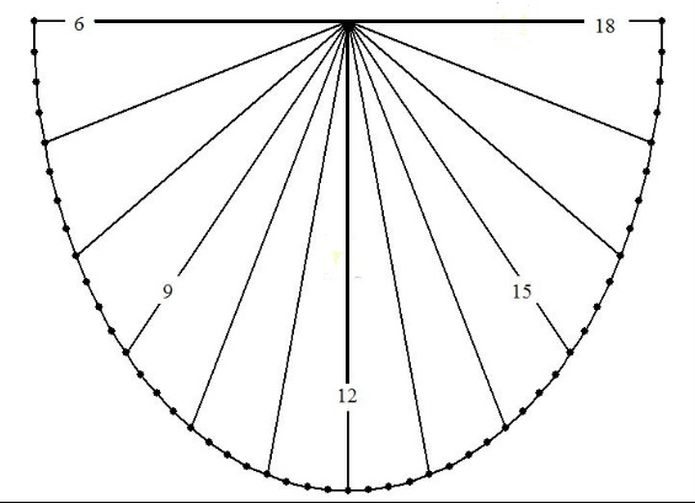 Abb.3 Zifferblatt für eine vertikale Sonnenuhr mit von einer halben Ellipse begrenzten Stundenlinien
Abb.3 Zifferblatt für eine vertikale Sonnenuhr mit von einer halben Ellipse begrenzten Stundenlinien
siehe auch: links im Bild 19 der o.g. Arbeit
↑↑ Anfang
<< andere Sonnenuhren-Beiträge
<< Home