<< Home
<< andere Astronomie-Beiträge
↓↓ Ende
Die Kepler-Gleichung
für die Berechnung des Ortes eines Planeten auf seiner Bahnellipse zum Zeitpunkt t
Inhalt
1. Berechnung des Ortes eines Planeten auf seiner Bahnellipse zum Zeitpunkt t2. Berechnung der Zentrischen Anomalie
2.1 Geometrische Begründung der Kepler-Gleichung
2.2 Anmerkung zur Mittleren Anomalie
3. Berechnung der Wahren Anomalie
4. Literatur
5. Anmerkung
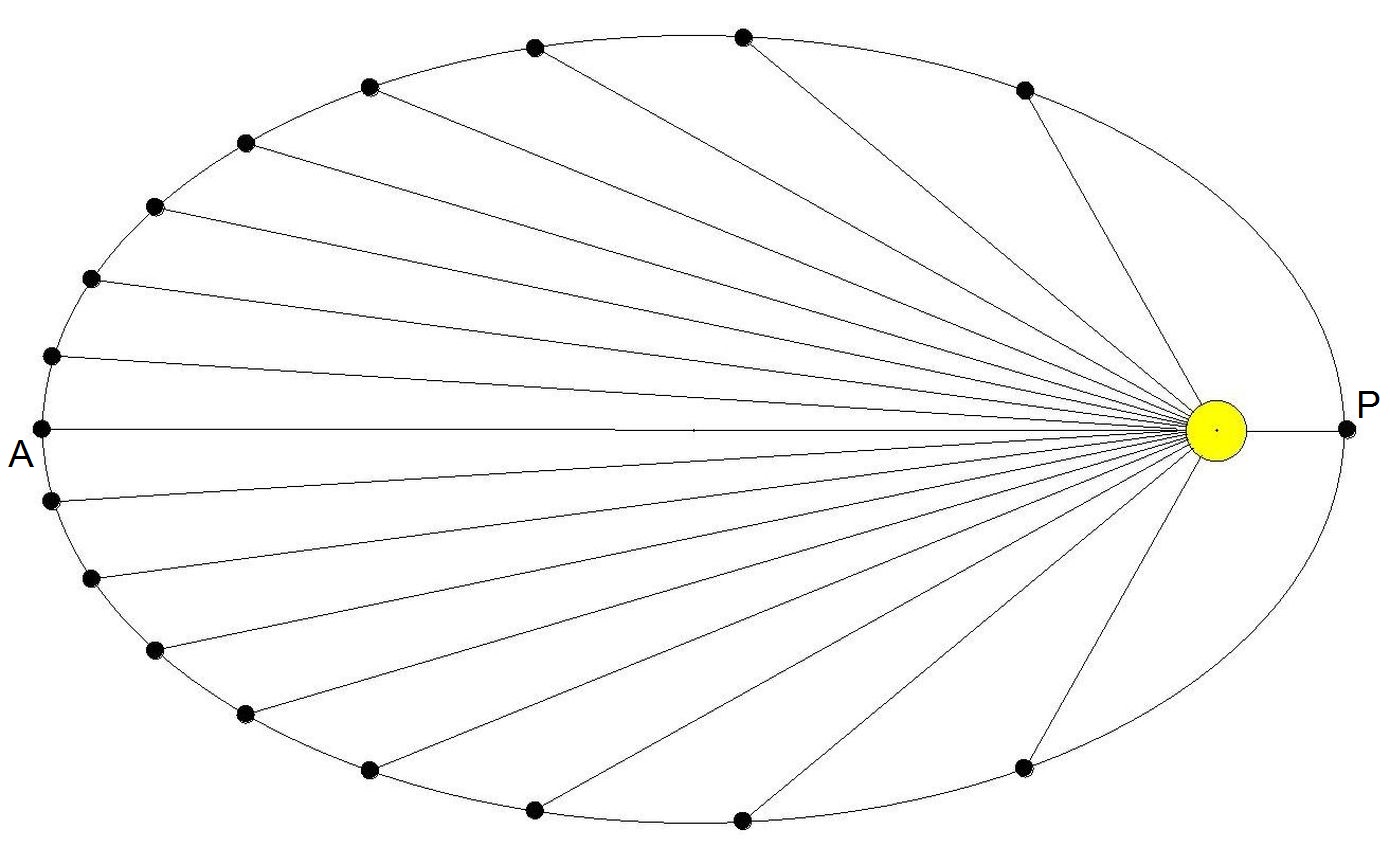Abb.1 nach gleichen Zeitintervallen aufeinanderfolgende Orte eines Planeten auf seiner elliptischen Bahn um die Sonne (im Beispiel je nach einem Achtzehntel der Zeit für einen Umlauf, z.B. vom Perihel zurück zum Perihel).
Die Fläche aller Sektoren ist gleich (im Beispiel ein Achtzehntel der Ellipsen-Fläche; ab Perihel-Durchgang wächst sie von Ort zu Ort um dieses Achzehntel).
1. Berechnung des Ortes eines Planeten auf seiner Bahnellipse zum Zeitpunkt t
Der Ort des Planeten auf seiner Bahnellipse zu einnem bestimmten Zeitpunkt ergibt sich gemäß zweitem Keplerschen Gesetz aus der in einem Zeitintervall vom Fahrstrahl zwischen Sonne und Planet überstrichenen Fläche. Ihre Größe ist proportional zur Zeit t . Das Zeitintervall beginnt im Moment eines bekannten Planeten-Ortes - vorzugsweise beim Passieren des Perihels - mit t= 0 .
Der von Kepler dafür gefundene Rechenweg besteht aus zwei Schritten:
1. Berechnung des Ellipsen-zentrischen Winkels E (Zwischengröße, Zentrische Anomalie) und
2. Berechnung des Sonnen-zentrischen Winkels V (Planeten-Ort, Wahre Anomalie) aus dem Winkel E.
Der 2. Schritt ist eine einfache trigonometrische Umrechnung, während Keplerim ersten Schritt eine nicht geschlossen lösbare Gleichung (transzendente Gleichung) hergeleitet und angewendet hat. Unter Kepler-Gleichung wird nur diese verstanden. Der Grund dafür kann sein, dass sie transzendent ist und schwerer zu finden war als die ihr nachfolgende Rechnung.
Die Aussagen in den zugrundeliegenden beiden ersten Keplerschen Gesetzen folgerte Kepleraus einer großen Zahl von Positionsmessungen der Planeten, insbesondere aus solchen vom Mars, die Tycho Brahe und er selbst jahrelang vorgenommen hatten. Wichtige Voraussetzung war, dass Keplernicht mehr im Geozentrischen Weltbild befangen, sondern vom Heliozentrischen Weltbild des Nikolaus Kopernikus überzeugt war.
Die Kepler-Gleichung und die nachfolgende Umrechnung sind das Ergebnis einer rein geometrischen Arbeit, bei der Keplerdie in seinen Beobachtungen zu findenden Regelmäßigkeiten in Form von Gleichungen darstellte. Mit deren Hilfe kann der Ort eines jeden Himmelskörpers, der auf einer Ellipse einen Zentralkörper umläuft, zu einem beliebigen Zeitpunkt vorausberechnet werden, wenn die Form der Ellipse und die Umlaufzeit T des Himmelskörpers auf ihr bekannt sind.
Die Form der Ellipse wird mit dem Verhältnis b/a (oder umgekehrt a/b) zwischen ihrer kleinen und großen Hauptachse bzw. ihre numerische Exzentrizität e beschrieben (Abb.2, links). Deren absolute Größen sind nicht erforderlich, wenn - wie meistens - vom Planeten-Ort lediglich die Polarkoordinate Richtungs-Winkel (Wahre Anomalie V), nicht auch der Abstands-Radius gesucht wird.
Anmerkung:
In der Astronomie wird das Formelzeichen e für die numerische Exzentrizität (eine relative, deshalb dimensionslose, nur mit einer Zahl bzw. einer Nummer angegebene Größe) und das Zeichen ε für die lineare Exzentrizität (eine absolute Größe mit Längen-Dimension) benutzt. Wegen der enormen Größe astronomischer Längenwerte, wird die lineare Exzentrizität wenig gebraucht, so dass mit dem Wort Exzentrizität i.d.R. die numerische E. gemeint ist.
Im Allgemeinen - so in der Mathematik - werden die beiden Formelzeichen in umgekehrter Bedeutung gebraucht.
Die physikalische Ursache erkannte später erst Newton. Er formulierte sie in seinem Gravitationsgesetz und zeigte, dass dieses und das zweite Keplersche Gesetz auch für die Bewegungen auf den anderen Himmelsbahnen (Parabeln und Hyperbeln) gelten.
2. Berechnung der Zentrischen Anomalie
Die Zwischengröße Zentrische Anomalie E wird für den Zeitpunkt t mit der Kepler-Gleichung berechnet. Diese lautet:
E - e sin E = M .
Im Ausdruck M (Mittlere Anomalie) ist die vorgegebene Variable t mit den Konstanten T und 2π zusammengefasst.
Die ausgeschriebene Kepler-Gleichung lautet:
E - e sin E = 2 π t/T .
Die Zentrische Anomalie E ist ein Winkel mit seinem Scheitel im Zentrum der Ellipse (Abb.2, links).
2.1 Geometrische Begründung der Kepler-Gleichung
Der Fahrstrahl von der Sonne S zum Planet hat zwischen seiner Lage im Perihel A (Beginn der Zeitzählung: t=0) und seiner Lage P im Zeitpunkt t die mit dem Winkel V gekennzeichete Teil-Fläche der Ellipse überstrichen (Abb.2, links und Mitte). Die Größe der Fahrstrahl-Fläche ist leicht berechenbar, der Winkel V daraus aber nicht direkt bestimmbar. Kepler fand heraus, das Letzteres auf dem Umweg über die berechenbare Lage des zu P auf dem Umkreis affinen Punktes P' möglich ist. Die dafür zu berechnende Größe ist der Richtungswinkel E des Punktes P' (Abb.2, links).
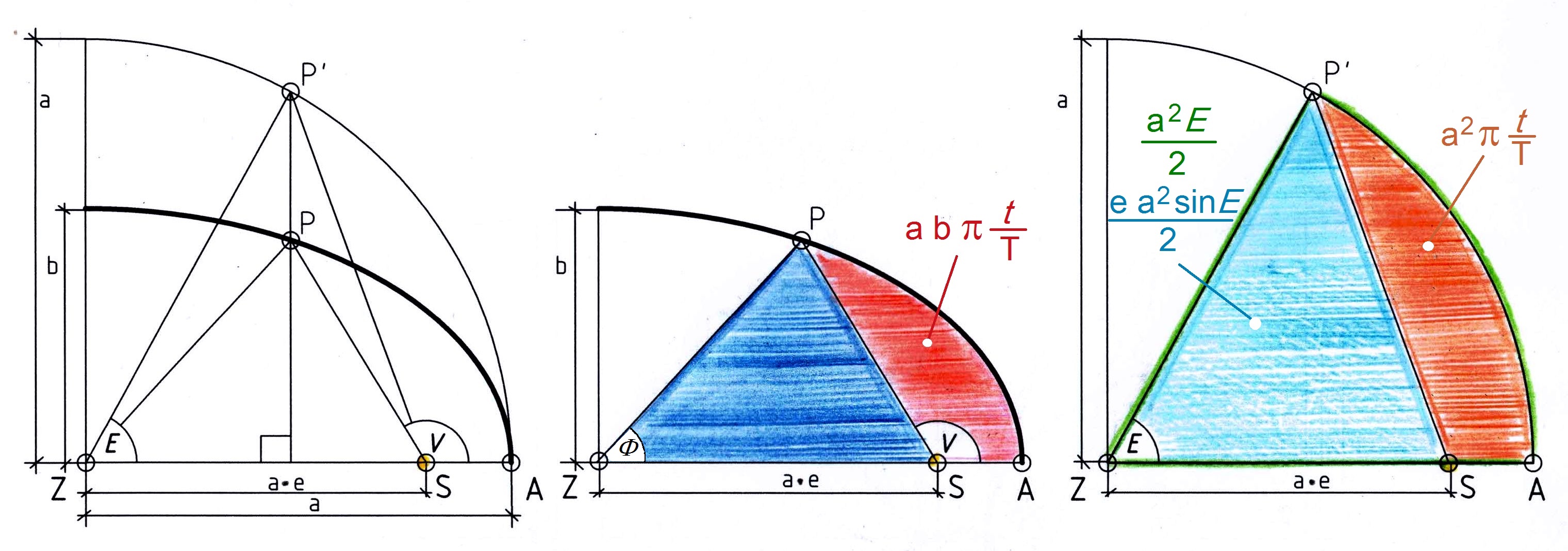Abb.2 links: Ein Planet befindet sich im Zeitpunkt t am Ort P seiner elliptischen Bahn um die Sonne; die von ihm überstrichene Fläche (Fahrstrahl-Fläche) ist mit dem Winkel V gekennzeichnet.
Zudem ist die "Fahrstrahl-Fläche" affin auf den Umkreis abgebildet (P' = Spitze der affinen Fahrstrahl-Fläche).
Der vom Zentrum Z zum Punkt P' führende Strahl begrenzt einen Kreissektor mit dem Zentriwinkel E.
Mitte: Die Fahrstrahl-Fläche ist rot markiert.
rechts: Der Kreis-Sektor ist grün und die affine Fahrstrahl-Fläche ist braun markiert.
Der Kreis-Sektor besteht aus der affinen Fahrstrahlfläche und einer cyan markierten Dreiecksfkläche
(die kleinere, zur Ellipse gehörende, also nicht verzerrte Dreiecks-Fläche (blau) befindet sich im mittleren Bild).
Die Fahrstrahl-Fläche ist:
FASP = a b π t/T . (Abb.2, Mitte).
Sie ist ein Sektor der Ellipsen-Fläche a b π. Ihr Anteil an dieser ist t/T.
Die bis zum Ellipsen-Umkreis verzerrte affine Fahrstrahl-Fläche ist gemäß der Affinität zwischen Ellipse und Umkreis:
FASP' = a2 π t/T . (Abb.2, rechts).
Sie ist die mit dem Affinitätsfaktor a/b vergrößerte Fahrstrahl-Fläche.
Der Kreis-Sektor ist Teil der Umkreis-Fläche:
FAZP' = a2 E / 2. Umkreis-Fläche = a2 π Anteil-Faktor = E / (2 π)
Die Dreieckfläche ist:
FSZP' = e a2 sinE / 2 Grundseite= e a Höhe = a sin E
Schreibt man die affine Fahrstrahl-Fläche als Differenz zwischen Kreis-Sektor und Dreieckfläche
(in Abb.2, rechts ist die Zusammensetzung erkennbar)
FAZP' - FSZP' = FASP' ,
so ist das bereits die Kepler-Gleichung, denn der verwendete Kreissektor und die verwendete Dreiecksfläche sind zu den entsprechenden Flächen in der Ellipse (Abb.2, Mitte) ebenfalls affin (Anmerkung).
Die bekannte Form entsteht, wenn man die Werte für die drei Flächen einsetzt:
a2 E /2 - a2 e sinE / 2 = a2 π t/T ; und nach Kürzen mit ½ a2:
E - e sin E = 2 π t/T.
Bei Verwendung von M (= 2 π t/T) auf der rechten Gleichungsseite ensteht die Kepler-Gleichung in der bekannten Form:
E - e sin E = M, q.e.d.
2.2 Anmerkung zur Mittleren Anomalie
In der Literatur wird gelegentlich versucht, die Mittlere Anomalie in den zur Herleitung der Kepler-Gleichung benutzten Zeichnungen ebenfalls unterzubringen, obwohl das nicht erforderlich ist und manchmal sogar Verwirrung stiftet [3].
Kepler hat mit M seine Gleichung lediglich ein wenig kürzer geschrieben. M ist nur indirekt die bei ihrer Anwendung vorzugebende Variable. Direkt wird der Zeitpunkt t vorgegeben.Man kann sich M als einen "Winkel im Bogenmass denken, der proportional mit der Zeit t wächst" [1]. Direkter gesagt: Der Ausdruck M =2 π t/T auf der rechten Seite der Gleichung ist genau so wie E auf der linken Seite ein Winkel im Bogenmaß. Beides sind Anomalien, die von Kepler als Exzentrische und als Mittlere Anomalie bezeichnet wurden.
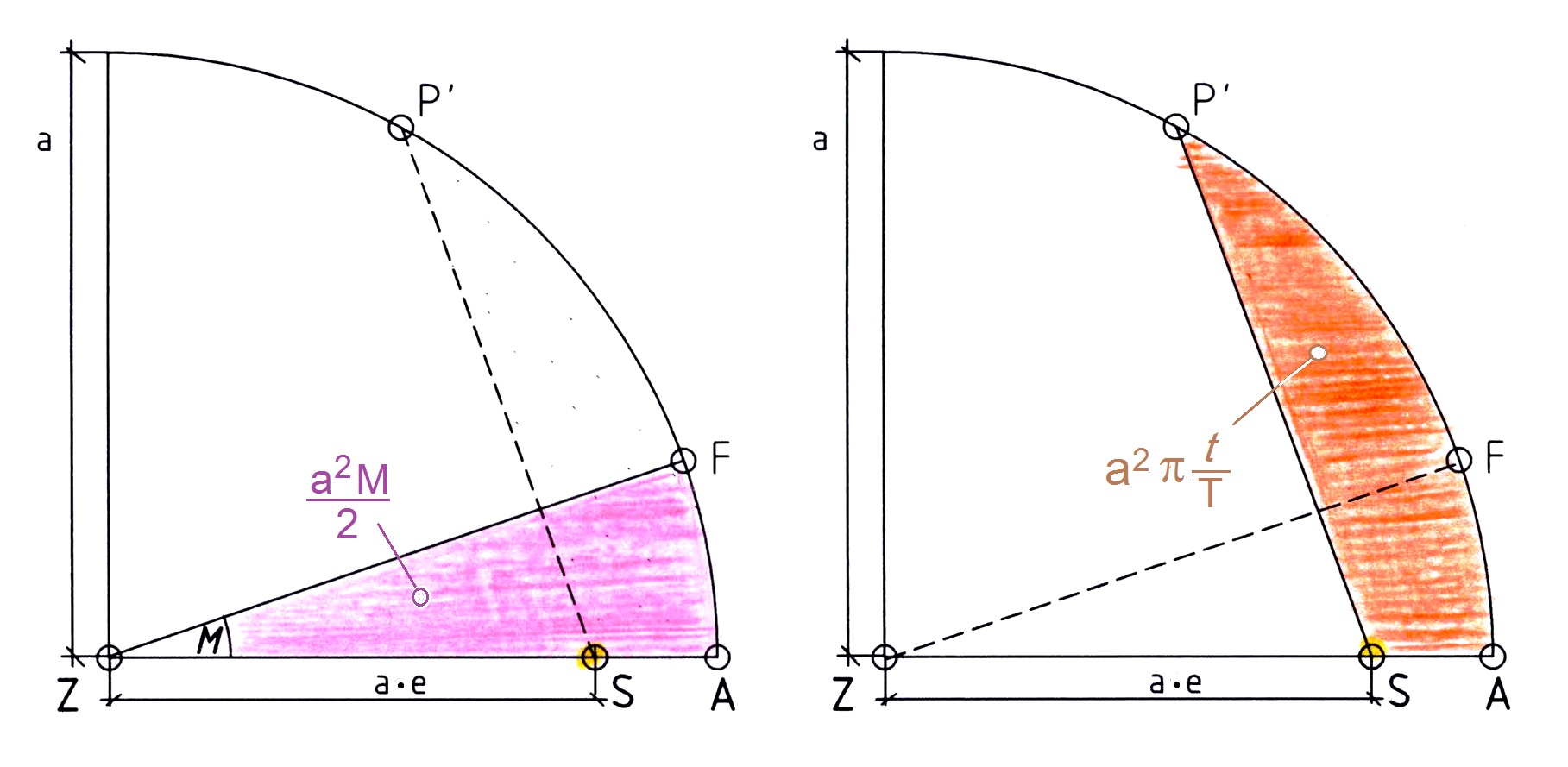
Abb.3 Die "M-Fläche" und die affine Fahrstrahl-Fläche; beide sind gleich groß
Wenn man mit diesem Zentriwinkel einen Sektor im Umkreis bildet, dann ist dessen Fläche a2M/2 (Abb.3, links) gleich groß wie die affine Fahrstrahl-Fläche (Abb.3, rechts).
Kontrolle: für M seinen Wert 2 π t/T einsetzen >> a2 π t/T = affine Fahrstrahl-Fläche.
Man kann sich M auch als Richtungswinkel eines die Sonne auf einem Kreis umlaufenden fiktiven Planeten F denken. Dieser wäre wie der sich drehende Zeiger einer Uhr ein Modell für den gleichmäßigen Verlauf der Zeit.
3. Berechnung der Wahren Anomalie
Die Gleichung für die Berechnung des Sonnen-zentrischen Winkels V (Planeten-Ort, Wahre Anomalie) aus dem Ellipsen-zentrischen Winkel E (Exzentrische Anomalie) lautet:
tan(V/2)=((1+e)/(1–e))1/2 tan(E/2).
Sie ist eine einfache, geschlossen lösbare Gleichung [2].
4. Literatur
[1] T. P. Wihler und H. R. Schneebeli:Von den Keplergesetzen zur Keplergleichung und zum Planetenort,
2. Geometrie der Planetenbewegung: Keplergleichung
[2] Siegfried Wetzel:
Die Zeitgleichung für Nicht-Astronomen,
Anhang 3: Von Anomalie E zu Anomalie V
[3] Rainer Stumpe:
Definition der mittleren Anomalie bei Kepler
5. Anmerkung
Es stellt sich die Frage, ob die Aufgabe auch ohne Anwendung der Affinität zwischen Ellipse und Umkreis lösbar wäre. Wollte man z.B. die von der Ellipse eingeschlossenen 3 Flächen (unverzerrte Fahrstrahl-Fläche, Fläche des unverzerrten Dreiecks und des aus beiden ersteren Flächen bestehenden Ellipsen-Sektors, s. Abb.2, Mitte) gegeneinander verrechnen, so müssten die beiden letzteren Flächen in einfacher Form mit dem Winkel Φ ausdrückbar sein Das ist aber nicht der Fall, und es ist üblich, solche i.d.R. längeren Ausdrücke durch Anwenden der genannten und bereits von Kepler benutzten Affinität zu finden.
Siegfried Wetzel, CH 3400, Juli 2025 (Dez.25)
↑↑ Anfang
<< andere Astronomie-Beiträge
<< Home