<< Home
<< andere Mechanik-Beiträge

 ↓↓ Ende

Balken: Biegen und Scheren

Inhalt

1. Einleitung
2. Biege- und Scher-Experiment
    2.1 Versuchsaufbau
    2.2 Das Biege-Experiment
    2.1 Das Scher-Experiment
    2.2 Vergleich der experimentellen Ergebnisse
3. Balkentheorie
    3.1 Biegen
    3.2 Scheren
    3.3 Vergleich der theoretischen Ergebnisse
4. Schlussbemerkung
5. Anmerkungen

1. Einleitung  ↑ Anfang

Bei Biegeuntersuchungen von Balken wird neben dessen Biegemoment- oft auch dessen Querkraft-Beanspruchung genannt (beispielsweise in Abb.1, Diagramm (Q(x)), auf letztere aber im Weiteren nur selten eingegangen. Mitunter wird lapidar bemerkt, sie spiele gegenüber der Beanspruchung durch das Biegemoment eine untergeordnete, d.h. eine vernachlässigbare Rolle.

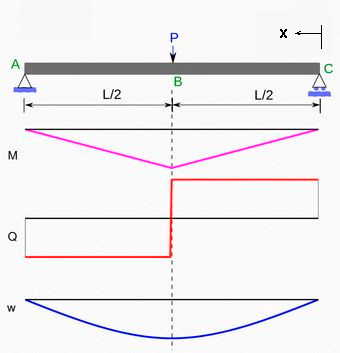<<< Abb.1  Balken auf zwei Stützlagern (Einfeldträger)

       P: mittige Last
       M: Moment über x   (M=½·P·x;  x=0 ...L/2)
       Q: Querkraft über x  (Q=P;         x=0 ...L/2)
       w: Durchbiegung über x (Biegelinie)

       Bild aus Wikipedia/Bbanerje

Die quer wirkende äußere Kraft P bewirkt nämlich nicht nur, dass sich der Balken verbiegt, sondern auch, dass sich seine Querschnitte parallel gegeneinander verschieben (Querschub, Scherung). Ein zwischen zwei Querschnitten befindliches Balkenelement wird in sich verzerrt. Ein sehr kurzer Balken kann auf diese Weise in Teile zerschert bzw. zerschnitten werden. Beim reinsten Schervorgang in einer Schere ist die betrachtete Balkenlänge auf die Breite des Messerspaltes geschrumpft (L/2 → 0). Über diese kurze Länge und mit großer Kraft P wird der Balken in Querrichtung stark verzerrt und schließlich getrennt bzw. zerschnitten.

In der Praxis ist ein Balken oder Stab "schlank", d.h. seine Länge ist wesentlich größer als seine Höhe oder Dicke. Und die Erfahrung lehrt, dass er sich unter üblicher Belastung (z.B. unter Einzellast wie in Abb.1) verbiegt und bei Überlastung nicht zerschnitten wird, sondern dass ein Biegebruch (i.d.R.durch Zerreisen auf der Außenseite der Biegekrümmung eingeleitet) erfolgt. Die Verschiebung w ist i.d.R. deutlich erkennbar. Zudem haben wir die Angewohnheit, einen Stab in Teile zu zerlegen, indem wir ihn übers Knie legen und zerbrechen. Die zum Abscheren nötigen Kräfte übersteigen die beim Biegebrechen anzuwendenden erheblich, so dass kaum jemand im Alltag das Scheren versucht, indem er den Stab mit beiden eng aneinander liegenden Fäusten fasst und die Fäuste parallel gegeneinander bewegt (nicht einmal ein Schnittversuch mit dem Taschenmesser verspricht leichten Erfolg).

Ich werde die bei der Belastung (= quer wirkende äußere Kraft) eines schlanken Balkens entstehenden Beanspruchungen (= Biegen und Scheren), die Spannungen im Balken und seine Verformung unter Anwendung der Balkentheorie bestimmen. Vorher beschreibe ich einfache schematisierte Experimente an einem (nicht einmal besonders) schlanken Balken, deren Ergebnisse ich mit den später ausgerechneten Werten vergleichen werde. Beides - Balkentheorie und Experimente - sollen den Grad vernachlässigbarer Scherbeanspruchung anschaulich machen.

2. Biege- und Scher-Experiment  ↑ Anfang

2.1 Versuchsaufbau  ↑ Anfang

Gewählt ist ein links eingespannter Balken (Kragträger), der sich gleich verhält, wie die rechte Balkenhälfte in Abb.1 bei umgkehrter Last-Richtung (bei C wirke F = P/2 nach unten). Biegen und Scheren werden getrennt voneinander nachgebildet: Abb.n 3 u. 4)

Der Balken ist längs in vier gleiche Abschnitte geteilt. Seine real homogene Elastizität wird in der Mitte jedes Abschnitts, wo der Balken jeweils zerschnitten ist, konzentriert vorliegend angenommen und mit Schraubenfedern simmuliert.Die Balkenklötzchen bleiben bei den im Experiment auftretenden relativ kleinen Kräften praktisch unverformt.

Abb.2 zeigt die Verbindungsgelenke zwischen den Klötzchen und die an den Schnittstellen wirkendenen Federn.

Abb.2  Details im Experiment-Aufbau
            links: Biegen (Drehgelenk, Zugfeder zwischen 2 Nägeln, Druckfeder zwischen 2 Bohrungsböden)
            rechts: Scheren (Schiebegelenk, Druckfeder zwischen 2 Nasen)
                alle Federn mit gleicher Kennlinie (2N/mm)

2.2 Das Biege-Experiment (Abb.3)  ↑ Anfang

Das Scheren durch die am freien Ende des Balkens quer wirkende Kraft F ist mittels Drehgelenken zwischen den Holzklötzchen ausgeschaltet (wird nicht simuliert). Die Klötzchen können sich nur (im Uhrzeigersinn) drehen, wenn sie das Biegemoment x·F schrittweise nach links weiter geben, sich aber nicht quer zueinander verschieben.

Jedes Klötzchen ist relativ zu seinem Nachbar umso mehr verdreht, je weiter links es sich befindet. Das zeigt, dass das Biegemoment mit der Entfernung x (Hebelarm) von der quer wirkenden Kraft F wächst (x von rechts nach links wachsend), und dass sich dementsprechend die Krümmung der Biegelinie vergrößert (s.auch Abb.1).

An den Schnittstellen bilden die Federkräfte ein Kräftepaar als Reaktionsmoment zum Biegemoment x·F. Der Abstand zwischen den Federn beträgt 2/3 der Balken (Klötzchen-)Höhe (Diskussion unter 3.1.5).

Abb.3  Biege-Verformung eines links eingespannten Krag-Balkens, Experiment mit Federn zwischen diskreten
           starren Abschnitten
           oben: unbelastet (kleine Verformung infolge Eigengewicht)
           unten: mit 1,1N belastet (verformt: f ≈ 53mm am Lastpunkt)
                     (≈0,1N = Gewichtskraft von Last-Stab und -Teller)

2.3 Das Scher-Experiment (Abb.4)  ↑ Anfang

Das Biegen durch die am freien Ende des Balkens quer wirkende Kraft ist mittels Querführung der Holzklötzchen auf dünnen Stangen (Velo-Speichen) ausgeschaltet (wird nicht simuliert). Die Klötzchen können sich nur quer verschieben, sich aber nicht (im Uhrzeigersinn) drehen, wenn sie die Kraft F schrittweise nach links weiter geben.

Jedes Klötzchen ist relativ zu seinem Nachbar gleich weit verschoben. Das zeigt, dass F eine über die Balkenlänge konstante Belastung ist (s.auch Abb.1), die folglich an jeder Stelle die gleiche Scherung erzeugt.

Abb.4  Scher-Verformung eines links eingespannten Krag-Balkens, Experiment mit Federn zwischen diskreten
           starren Abschnitten
           oben: unbelastet
           unten: mit 10,1N belastet (verformt: f ≈ 20mm)
                     (≈0,1N = Gewichtskraft von Last-Stab und -Teller)

2.4 Vergleich der experimentellen Ergebnisse  ↑ Anfang

2.4.1 Vergleich der Messergebnisse

Dass im Scher-Experiment im Vergleich zum Biege-Experiment bei sogar etwa 9,2-facher Last F (10,1N/1,1N ≙ 1010g/110g) die Verschiebung w nur etwa 38% (21mm/50mm) ist, zeigt die Berechtigung, dass die Scherkraft-/"Querkraft"-Beanspruchung eines schlanken Balkens im Vergleich zu seiner Biegebeanspruchung im Allgemeinen vernachlässigt werden darf.
Bei gleicher Last verhalten sich die Verschiebungen aus Scherung und Biegung wie 1 zu 22.

2.4.2 Vergleich der Ergebnisse unter Beachtung der Federraten

Die Verwendung von zwei Federn an jeder Schnittstelle im Biege-Experiment war eine praktische Notwendigkeit: je eine für die Zug- bzw. Druckseite im Balken. Im Scher-Experiment genügte wegen nur einer vorkommenden Spannungsrichtung auch nur eine Feder in jeder Schnittstelle. Aus praktischen (Beschaffungs-) Gründen wurden in beiden Fällen Federn mit gleicher Federrate verwendet.
Die Federn ersetzen die Ellastizität des Balkenmaterials. Bei guter Realnähe sollten sich die Federraten wie die Werte von Elastizitätsmodul E (Normal- bzw. Zug- und Druckspannungen) und Gleitmodul (Schubspannungen), also für Stahl wie 2,6 zu 1 verhalten. Das tatsächliche Verhältnis in den Experimenten war 2 zu 1.
Die eine Feder im Scher-Experiment war um den Faktor 1,3 zu steif (2,6/2; oder umgekehrt: die beiden Federn im Biege-Experiment um den Faktor 0,77 zu weich). Nach entsprechender Korrektur ist das o.g. Verhältnis der Verschiebungen aus Scherung und Biegung wie 1 zu 16,9.

3. Balkentheorie  ↑ Anfang

Scheren kommt fast immer gemeinsam mit Biegen vor, weil ein Balken i.d.R. mit einer quer zu seiner Achse wirkenden Kraft verbogen wird (Abb.5, links). Wegen dieser "Normalität" wird wie in der Praxis auch in der Balkentheorie meistens nicht darauf eingegangen, aber auch unterschlagen, dass es somit fast immer - wenn auch in unbedeutetem Maße - vorhanden ist. Erst bei intensiverem Literaturstudium findet man Genaueres, nämlich die Begriffspaare Querkraftbiegung und reine Biegung. Bei Letzerer ist die Belastung ausschließlich ein Biegemoment (Abb.5, rechts), Scheren kann nicht übergangen werden, da es nicht auftritt.

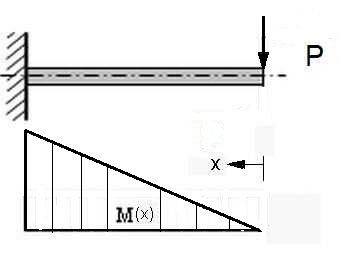
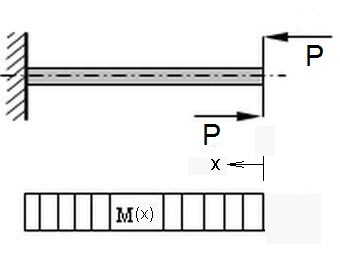Abb.5  Biegebeanspruchung eines Balkens
       links: Querkraftbiegung mit Querkraft P
       rechts:reine Biegung mit Kräftepaar P -  P

Ich werde auf die reine Biegung nicht weiter eingehen (nur diese Bemerkung: Die Biegelinie ist kreisförmig). Bei der Querkraftbiegung werde ich Biegen und Scheren getrennt voneinander behandeln. Einerseits folge ich den oben getrennt vorgenommenen Experimenten, andererseits kann ich beide Effekte am Ende überlagern (superpositionieren), da sie als voneinander unabhängig betrachtbar sind.
Im Experiment ist das Biegemoment wie in Abb.5, links linear ansteigend vom Kragbalkenende bis zur Einspannstelle (in Abb.5, rechts: über die gesamte Balkenlänge konstant).

Meine balkentheoretischen Bemühungen sollen
* einerseits die Theorie auffrischen helfen (eingeschränkt auf einen Kragbalken mit konstantem und rechteckigem
   Querschnitt über seine ganze Länge) und
* andererseits rechnerische Ergebnisse zum Vergleich mit den Ergebnissen aus den o.g. Experimenten liefern.

3.1 Biegen  ↑ Anfang

Quantitatives Arbeitsziel ist die Biegung w des Kragbalkens als Funktion der an seinem Ende wirkenden Kraft F.

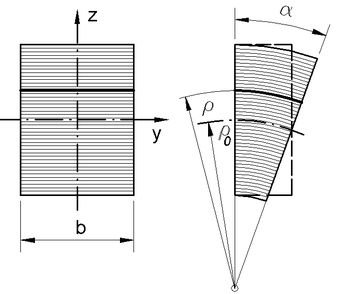<<< Abb.6  Gebogenes Balkenstück

3.1.1 Balken als Stapel dünner elastischer Bänder

Der Balken lässt sich als Stapel aus differentiell dünnen Längsbändern der Breite b (= Balkenbreite, Anmerkung 1) auffassen. Beim Biegen um eine horizontale Achse werden die Bänder im Bogen-Außenteil gedehnt (Zugspannung in ihnen erzeugt) und die im -Innenteil gestaucht (Druckspannung in ihnen erzeugt). In Abb.6 ist unmaßstäblich ein differentiell kurzes (α << 1) gebogenes Balkenstück dargestellt.

3.1.2 Dehnung und Krümmung

Im gebogenem, differentiell kurzem Balkenstück ist eine Beziehung zwischen den Dehnungen/Stauchungen und der Krümmung herzustellen.

Die ursprünglich von Jacob Bernoulli (1655 - 1705) formulierten, in guter Nöherung gültigen Annahmen, dass rechtwinklig quer liegende Ebenen beim Biegen eines schlanken Balkens (Länge >> Querabmessungen) eben und rechtwinklig zur Balkenachse bleiben, sind in Abb.6 berücksichtigt.

Die relative Dehnung ε des Bands mit der Höhen-Koordinate z ist:
ε = (α·ρ_z - α·ρ₀) / α·ρ₀ = (ρ_z - ρ₀) / ρ₀ = -z / ρ₀,
(1)   ε(z)= z / ρ₀

3.1.3 Spannungen und Krümmung

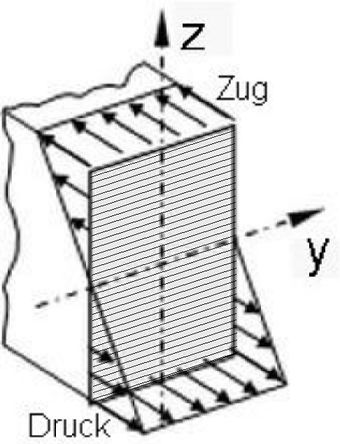<<< Abb.7  lineare Verteilung der Spannung über der Balkenhöhe

Mit dem Hooke'sches Gesetz (Anmerkung 2):
(2)   ε · E = σ
(Proportionalität zwischen ε und Spannung σ, unter der die Bänder stehen; Werkstoffkonstante Elastizitätsmodul E als Proportionalitätsfaktor)
ergibt sich mit Gl. (1):
(3)   σ(z) = E·z / ρ₀.

Diese Gleichung zeigt die lineare Verteilung der Spannung über der Balkenhöhe (z-Koordinate, Abb.7). Ihre Steigung 1 / ρ₀ enthält den für die Beschreibung der Biegung gesuchten Krümmungsradius ρ₀. Um ihn aus Gl. (3) zu erhalten, ist die Größe der Spannung σ(z) zu ermitteln.

3.1.4 Schwerpunkt der Schnittfläche und Nullpunkt der Koordinate z

Zunächst wird noch der Nachweis erbracht, dass es richtig war, den Nullpunkt der Koordinate z in der Mitte der Balkenhöhe anzubringen (Abb.6):

In Abb.7 bleibt nur der rechte Teil des Balkens abgeschnitten, links setzt sich der Balken fort. In der verbleibenden Schnittfläche A stehen die Spannungen lediglich mit dem von außen wirkenden Biegemoment im Gleichgewicht. Als über die Fläche aufsummierte (Integral-Bildung) Normalkraft sind sie Null, was folgender Gleichung entspricht:
(4)   b ∫_z σ(z) · dz = 0.
Gl. (3) in (4) eingesetzt:
(E·b / ρ₀) ∫_z z·dz = 0 .
E und ρ₀ sind endliche Größen, also:
(5)   b ∫_x z·dx = 0         (Anmerkung 3).
Gl. (5) ist ein auf ihren Schwerpunkt bezogener geometrischer Ausdruck der rechteckigen Fläche A, ihr sogenanntes Flächenmoment 1. Ordnung. Der Punkt z = 0 , für den Gl. (5) gilt, ist somit der Flächenschwerpunkt. Er liegt in der Mitte der Höhenausdehnung von A, und ist in Abb.6 bereits als Koordinaten-Ursprungspunkt verwendet.

3.1.5 Biegemoment und Krümmung

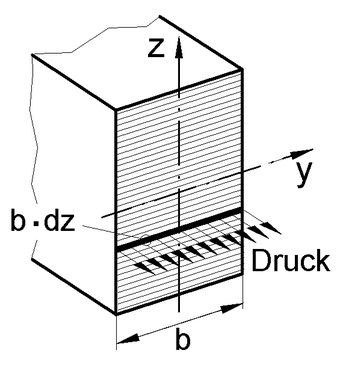<<< Abb.8  Spannung dσ eines Längsbandes und dessen Abstand z
       vom neutralen Band

Die Teilmomente  dM' = b·dσ(z)·z  jedes Längsbandes ergeben aufsummiert (Integral-Bildung) das Reaktionsmoment zum von außen angelegten Moment  M:
(6a)   b ∫_x σ(z)·z·dz = M;
wird mit Gl. (3) zu:
(E· b / ρ₀) ∫_x z²·dz = M .
Mit b ∫_xz²·dz = J_y = Flächenträgheitsmoment bzw. Flächenmoment 2. Ordnung von A lautet das Ergbnis für den Krümmungsradius an der Stelle x:

(6)   ρ₀ = E·J_y / M(x)_y   (Balken konstanten Querschnitts: J_y ist von x unabhängig).

Einschub:
Im Experiment habe ich die Wirkungslinien der beiden Federn im Abstand von je 2/3 der halben Balkenhöhe von der Balkenmitte aus, d.h. durch den Schwerpunkt der dreieckigen Spannungsfächen führend, angebracht (Abb.2, links). Wird diese zunächst intiutive Entscheidung von der Theorie gestützt?
Die Gleichung σ(z) lautet mit dem Randwert σ_R = σ(z_R):
σ(z) = (σ_R / z_R) · z .
Eingesetzt in Gl (6a):
M = (b·σ_R / z_R) ∫_zRz²·dz .
Ausgerechnet:
M = b·σ_R·z²_R / 3 .
Dieses Ergebnis lässt sich zum Moment als Produkt aus Hebelarm  z_R· 2/3  und Kraft  b·σ_R·z_R· 1/2  umschreiben.
Damit ist bestätigt:
Platzierung der Federn auf 2/3 der halben Balkenhöhe,
jede Feder wirkt als Resultante der beidseitig linear (Dreieckfläche) ansteigenden Spannungen.

3.1.6 Biegelinie und biegende Kraft am Balkenende

Der Kehrwert des Krümmungsradius ist die zweite Ableitung nach x der Ausbiegung (Biegelinie) w des Balkens:
1 / ρ = w(x)'' = M(x) /(E·J_y)
Zweimalieges Integrieren (und  M = F·x ) führt zur Gleichung der Biegelinie w(x):
w'(x) = (F / (E·J_y)) ∫_x x·dx = (F / (E·J_y))·(x²/2 + C₁),         x=L: w'= 0  →  C₁ = - L²/2 ;
 w(x) = (F / (E·J_y)) ∫_x (x²/2 + L²/2) dx = (F / (E·J_y))·(x³/6 + x·L²/2) + C₂,         x=L: w= 0  →  C₂ = L³/3 ;
(7)   w(x) = (F / (E·J_y)) · (x³/6 - x·L²/2 + L³/3)

3.1.7 Durchbiegung am Ort der biegenden Kraft

3.2 Scheren  ↑ Anfang

Quantitatives Arbeitsziel ist die Scherung s des Kragbalkens als Funktion der an seinem Ende wirkenden Kraft F.

3.2.1 Balken aus elastisch quer verschieblichern dünnen Schichten, Gleitwinkel und Schubspannung

Im Gegensatz zur reinen Biegung gibt es die reine Scherbeanspruchung des Balkens nicht. Der Hebelarm (anschaulich: der Spalt zwischen den Messern einer Schere) müsste verschwinden können, damit eine Querkraft nicht immer auch den Balken verbiegt (Anmerkung 4). Die in Abb.9 dargestellte Scherverformung eines kurzen Kragbalkens zu einem Körper mit Parallelogramm-Umriss ist lediglich gedanklich postuliert. Der eingezeichnete sogenannte Gleitwinkel γ ist eine formale, nicht messbare geometrische Größe.

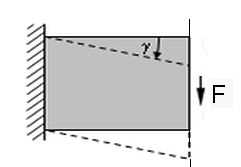
↑ ↑ Abb.9  Scherverformung eines kurzen Kragbalkens
                   zu Körper mit Parallelogramm-Umriss
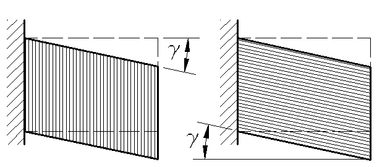
                   Abb.10  Scherverformung als Gleiten vertikaler oder horizotaler Schichten aufeinander ↑ ↑

Die Querkraft F bewirkt (neben dem Biegen des Balkens) gegenseitiges elastisches Verschieben gedachter benachbarter dünner Querschnitt-Scheiben oder übereinander liegender Längsscheiben des Balkens und Erzeugen von Scher- oder Schubspannungen τ zwischen ihnen (Anmerkung 5).

3.2.2 Gleitwinkel, Schubspannung und Gleitmodul

Der Gleitwinkel γ und die Schubspannung τ sind mittels der Materialkenngröße Gleitmodul G, die sich aus dem sogenannten rechnerisch verallgemeinerten Hooke'schen Gesetz ergibt, miteinander verknüpft (Anmerkung 6):
(8)  τ = G·γ

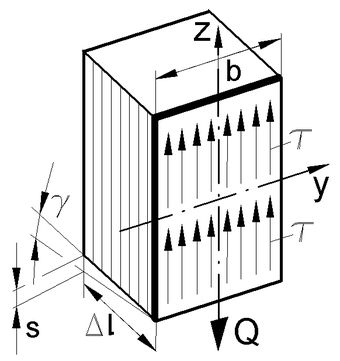<<< Abb.11  Schubspannung τ in der Balkenschnittfläche A

3.2.3 Schubspannung und Querkraft

Über die Balkenbreite ist die Schubspannung τ in guter Näherung konstant, über die Balkenhöhe ist sie parabelförmig verteilt (an den Rändern Null, in der Mitte maximal, Anmerkung 7). Sie zeigt in z-Richtung entgegen der äußeren Querkraft F. Im Folgenden wird in grober Näherung mit über die Fläche A gleichmässig verteilter mittlerer Schubspannung τ_m als Quotient aus Querkraft F und Fläche A gerechnet:
(9)  τ_m = F / A
Am Ende wird das Ergebnis mit dem sogenannten Schubbeiwert korrigiert
(Anmerkung 8).

3.2.4 Querkraft und Querverschiebung

Die Querverschiebung s wird mit folgender Beziehung ausgedrückt (Abb.11):
s = Δl·tanγ ≈ Δl·γ
Mit den Gleichungen (8) und (9) wird daraus:
(10)  s = Δl·F / (A·G) .

3.2.5 Querverschiebung und scherende Kraft am Balkenende

Die auf Δl bezogene Querverschiebung ist über die Balkenlänge konstant. Am Balkenende ist:
s = L·F / (A·G) .

3.3 Vergleich der theoretischen Ergebnisse  ↑ Anfang

Für den Balken mit rechteckigem Querschnitt b·h sind
J_y = b·h³ / 12   und   A = b·h .

Durchbiegung w und Querverschiebung s am freien Ende des Kragbalkens sind:
w = 12·F·L³ / (3·E·b·h³),
s = L·F / (b·h·G)

Zwischen den Materialkonstanten (für Eisen) besteht das Verhältnis:
E / G = 2,6·G / G = 2,6 .

Das Verhältnis zwischen Durchbiegung und Querverschiebung ist:
w / s = {12·F·L³ / (3·E·b·h³)}  /  { L·F / (b·h·G)}
w / s = {4·L² / (2,6·G·h²)}  /  { 1 / G}
w / s = (4 / 2,6) · (L / h)²

Für  L / h = 3,65  (entspricht Experiment-Vorgaben) verhalten sich die Verschiebungen aus Scherung und Biegung in grober Näherung wie 1 zu 20,5
und nach Korrektur mit dem Schubbeiwert κ=1,2 (s. Anmerkung 8) wie 1 zu 17,1.

4. Schlussbemerkung   ↑ Anfang

Dass ich fast gleiche Werte (16,9 bzw. 17,1) für das Verhältnis der Biege- zu den Scher-Verschiebungen aus Experimenten und Balkentheorie erhielt, ist erstaunlich. Primäres und erreichtes Ziel war aber, die Größenordnung des Verhältnisses einerseits balkentheoretisch, andererseits auch experimentell zu ermitteln.

5. Anmerkungen  ↑ Anfang

Anmerkung 1:
Die bei allgemeinem Balkenquerschnitt benutzte Vorstellung eines Faserbündels lässt sich wegen der konstanten Balkenbreite auf die eines Stapels von Bändern konstanter Breite reduzieren (Bänderstapel).

Anmerkung 2:
Der Elastizitätsmodul E wird in Dehnzugversuchen bestimmt: Mit Hilfe des Hooke'schen Gesetzes ergibt er sich aus Zugkraft pro Probenquerschnittsfläche und relativer Dehnung.

Anmerkung 3:
Die Breite b ist ebenfalls eine endliche Größe. Die Aussage der Gl. (5) ist auch ohne b gültig, was ich aber stehen liess, um den gängigen, allgemeinen Begriff des Flächenmomentes beizubehalten.

Anmerkung 4:
Im Scher-Experiment (Abb.4) sind die endlich langen Balkenstücke starr, wodurch das Funktionieren der zwischengefügten Schiebegelenke (Biegen bzw. Drehen der Balkenstücke verhindern) überhaupt erst möglich gemacht wird.

Anmerkung 5:
Der Schervorgang ist sowohl mit gegenseitigem Verschieben vertikaler als auch horizontaler Scheiben anschaubar zu machen. Man kann sich auch beide Vorgänge gleichzeitig stattfindend vorstellen, wenn man die beiden Scheibenpakete als sich durchdringend - ähnlich wie sich kreuzende Bänder aus parallelen Fäden - ansieht.
Nach dem Gesetz zugeordneter Schubspannungen treten ohnehin Schubspannungen immer paarweise rechtwinklig in gleicher Größe zueinander auf, also in gleicher Größe an den Schnittstellen vertikaler mit horizontalen Schichten.

Anmerkung 6:
Beim Dehnzugversuch wird zusätzlich die Querdehnung ν als Materialkonstante gemessen. Mit deren Hilfe wird
G zu:
G = E / (2(1+ν)) .

<<< Abb.12 Gummistreifen (30mmx14mm)
       oben: unbeansprucht, gerade Querlinie
       unten: scherbeansprucht, S-förmige Querlinie
                 (keine Biegebeanspruchung an dieser Stelle)

Anmerkung 7:
Am unteren und oberen Rand ist die Schubspannung Null, denn die benachbarten Scheiben finden kein Material mehr vor, mit dessen Hilfe sie sich gegenseitig festhalten könnten. Eine Analogie dazu ist eine oben gegen Luft endende Wand. Direkt an ihrem Rand hat kein Nagel mehr Halt, an dem z.B. ein Bild aufgehängt werden könnte.
Die Scheibenränder gleiten auch nicht gegeneinander, so dass der Schnittwinkel am Rand rechtwinklig beibt. Das hat zur Folge, dass die Bernoulli 'sche Annahme eben bleibender Schnitte nicht zutrifft: S-förmig verwundene Flächen (s. Abb.12)
Auch das äußerste der vorstellbaren horizontalen Bänder kann dem zweitäußersten keinen Halt mehr geben. Die Schubspannung an der Oberfläche ist Null.

Anmerkung 8:
Beachtet man den tatsächlichen parabelförmigen Verlauf der Spannungen über die Höhe mit der im Allgemeinen verwendeten Gleichung
(9a) τ = F S(z) / (J b)
(S(z) ist das Flächenmoment 1. Ordnung oder das statische Moment),
und benutzt den Ansatz für die Formänderungsarbeit, so errechnet man eine etwas größere Verschiebung (für den Rechteckquerschnitt ist der "korrigierende", sogenannte Schubbeiwert κ = 1,2).
Die Herleitung von Gl. (9a) wird übrigens durch Gleichgewichtsbetrachtung in einem horizontalen Schnitt mit Hilfe der zugeordneten Schubspannung vorgenommen.

Siegfried Wetzel, CH 3400 Burgdorf, Apr. 2016 (Jan.20, Febr.23)

 ↑↑ Anfang
<< andere Mechanik-Beiträge
<< Home