<< Home
<< andere Ostern-Beiträge
↓↓ Ende
Die Oster-Rechnung von Gauß
nachbetrachtet für Laien
(Astronomie + Raumfahrt im Unterricht, Heft 2, 2009, gekürzt)
Zusammenfassung
Carl Friedrich Gauß (1777 - 1855) stellt den Algorithmus der Oster-Rechnung, den computus, der schon seit dem frühen Mittelalter benutzt und anlässlich der Gregorianischen Kalender-Reform verfeinert wurde, mit den Mitteln Neuzeitlicher Mathematik dar. Er "will mit seiner Regel ganz bewusst ein praktisches Hilfsmittel an die Hand geben, das ohne die Kenntnis des in ihr komprimiert und verschleiert enthaltenen computus von jedermann angewendet werden kann" [1]. In der vorliegenden Arbeit soll der Schleier ein wenig gelüftet werden. Das Hauptziel wäre erreicht, wenn der Leser erkennt, wo und wie die als "Text-Prosa" bekannte Oster-Rechnung in die Formeln von Gauß eingeht. Die Absicht, alle mathematischen Regeln und Umformungen (es handelt sich im Wesentlichen um Modulo- und Integer-Rechnung) im Detail zu erklären, besteht nicht.
Inhalt
1. Einleitung
2. Der Meton-Zyklus
3. Die Oster-Grenze
4. Die Meton-Bilanz im Julianischen Kalender
5. Die Gauß'sche Zahl
6. Die Berechnung der Oster-Grenze
7. Die Berechnung der Sonntags-Distanz
8. Korrekturen durch die Gregorianische Reform: Sonnen- und Mondangleichung
9. Die korrigierte Oster-Grenze
10. Die korrigierte Sonntags-Distanz
11. Die Gauß-Formeln für den Julianischen und für den Gregorianischen Kalender
12. Ausnahmen in der Gregorianischen Oster-Rechnung
13. Literatur
14. Anmerkungen
Die allgemein bekannte Text-Formulierung der Oster-Regelung könnte lauten:
Ostern ist der erste Sonntag nach dem ersten Vollmond im Frühling.
Die Oster-Findung richtet sich aber nicht nach den tatsächlichen (astronomischen) Ereignissen Frühlings-Anfang und Frühlings-Vollmond. Die "amtliche" Oster-Rechnung (computus) der christlichen Kirche fixiert den Frühlings-Anfang auf den 21.März und sagt den Frühlings-Vollmond auf Grund eines aus vergangenen Beobachtungen gut bekannten Mittelwertes für die Mond-Monate (Lunationen) voraus.
In der Gegenwart (bereits seit dem Jahre 1900) lässt sich dieser Sonntag nach denselben einfachen Regeln wie vor der Kalender-Reform finden. Die 1582 vorgenommene Regel-Verfeinerung wird erst wieder ab dem Jahre 2100 wirksam.
Die noch fast ein Jahrhundert lang mögliche einfache Oster-Findung ist in Abb.1 [2] für ein paar Jahre dargestellt:
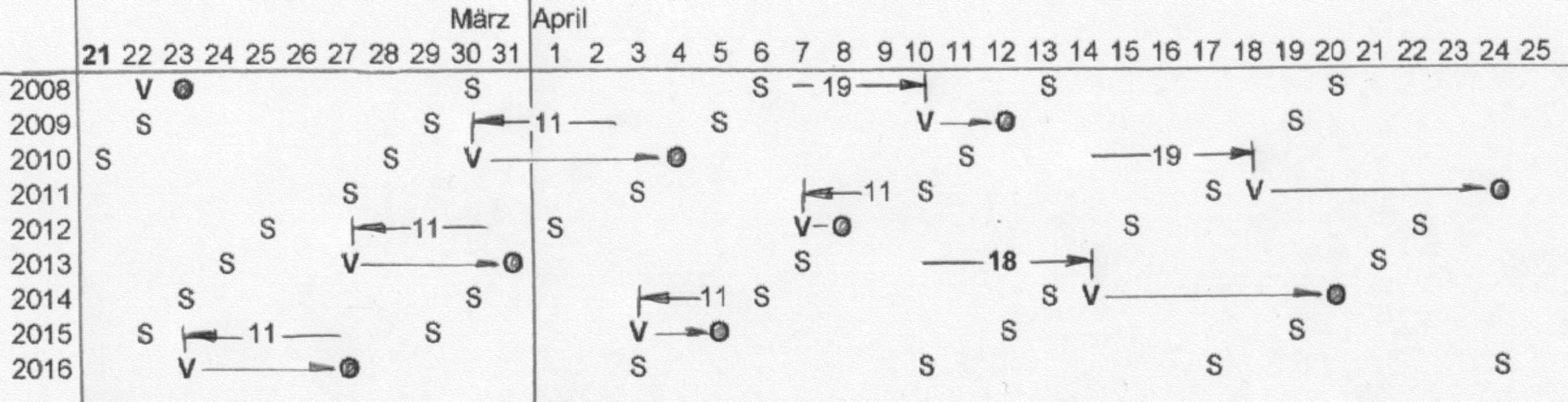Abb.1 Oster-Findung für die Jahre 2009 bis 2016 [2]
Frühlings-Vollmonde (V), Sonntage (S) und Oster-Sonntage (O)
- Als Tag des Frühlings-Anfangs wird immer der 21.März angenommen.
- Der für das nächste Jahr vorausgesagte Tag des Frühlings-Vollmondes V ist ein gegen über heuer 19 Tage späterer Kalender-Tag, aber ein 11 Tage früherer, wenn er dabei nicht vor den 21. März fällt.
- Nach 19 Jahren ist der Vollmond-Tag ausnahmsweise 18 Tage später als im Jahr vorher. Ende dieser gegenwärtigen 19-Jahre-Periode ist das Jahr 2014, das der späteren 2033, 2052 usf.
- Ostern O ist immer am nächsten Sonntag S nach dem Frühlings-Vollmond V.
- Die Sonntage S sind im nächsten Jahr je einen Tag früher als im Vorjahr, in Schalt-Jahren 2 Tage früher
(Anmerkung 1).
Für einige Jahrzehnte besteht keine Notwendigkeit sich mit den Gauß'schen Oster-Formeln im besonderen oder der Oster-Rechnung im allgemeinen zu befassen, es sei denn aus "akademischen Gründen", wie es im folgenden geschieht. Ausnahmeregeln werden erst in den Jahren 2049 und 2076 wirksam (s.12.).
2. Der Meton-Zyklus ↑ Anfang
Die oben schon genannte 19-Jahre-Periode hat ihren Namen nach dem griechischen Astronomen Meton (5.Jahrh.v.C.). Der mit unendlicher Dauer angenommene Meton-Zyklus war aber schon den Babyloniern bekannt. Er beschreibt die Beobachtung, dass nach einer Periode von19 Sonnen-Jahren j 235 Mondumläufe m (Lunationen) beendet sind, nach erneuten 19 Sonnenjahren wiederum 235 Mondumläufe, usf.. Für die Oster-Rechnung ist das eine Vereinfachung, nämlich die Beschränkung auf nur 19 mögliche Kalender-Tage für den Frühlings-Vollmond, der die Ostergrenze angibt (der Oster-Sonntag liegt 1 bis 7 Tage später als dieses Grenz-Datum). Nach je 19 Jahren beginnt das Mond-Verteilschema von neuem. Es zu ermitteln, ist unsere erste Aufgabe. Dabei bleiben wir zunächst beim Julianischen Kalender, respektive bei der Jahreslänge in Tagen, wie sie in diesem Kalender zur Oster-Rechnung verwendet wird:
19j = 235m = 19·365,25Tage = 6'939,75Tage.
3. Die Oster-Grenze ↑ Anfang
Meton hat das gesuchte Mond-Verteilschema für den Julianischen Kalender prinzipiell vorgegeben. Es laufen zwei unterschiedliche Jahre parallel, nämlich ein Sonnen- und ein Mondjahr. Beide werden mit Schalt-Tagen gemeinsam korrigiert. Dann wird das kürzere Mondjahr (354 Tage ≈ 12 Lunationen) dem Sonnenjahr angepasst, indem innerhalb von 19 Sonnenjahren 6 Schalt-Monate zu 30 Tagen und einer zu 29 Tagen angehängt werden. Das ergibt die in der Einleitung genannten Verfrühungen des Frühlings-Vollmondes von 11 Tagen oder Verspätungen von 19 resp.18 Tagen.
4. Die Meton-Bilanz ↑ Anfang
Bei Meton sieht die Bilanz auf 6'940 Tage (Anmerkung 2) so aus:
125 "lange" Monate zu je 30 Tagen = 3'750
110 "kurze" Monate zu je 29 Tagen = 3'190
Summe = 6'940
Über das Aussehen eines kompletten lunisolaren Kalenders von Meton ist nichts bekannt. Im Julianischen Kalender ist sowohl der Mond- als auch der Sonnen-Teil klar geregelt.
Die Schalttage korrigieren beide Kalender-Teile und erscheinen in der
Bilanz auf 6'939,75 Tage:
19 Mondjahre à 354 Tage = 6'726
6 Schalt-Monate à 30 Tage = 180
1 Schalt-Monat à 29 Tage = 29
4,75 Schalt-Tage im Durchschnitt = 4,75
Summe = 6'939,75 = 19·365,25 Tage = 19 j .
Ein Schalttag hatte in alter Zeit kein Datum. Er wurde lediglich als doppelt langer Tag behandelt. 1 Tag wurde spurlos eingefügt, ähnlich wie 1 Stunde bei der heutigen Umstellung auf Winterzeit. Heute ist er als 29.Februar klar erkennbar. Dennoch müssen die Schalttage in der obigen Bilanz als Extra-Tage aufgeführt sein, denn mit den verrechneten Mondjahren und Schalt-Monaten werden sie nicht erfasst.
5. Die Gauß'sche Zahl ↑ Anfang
Es ist fraglos praktisch, jeder der 19 Möglichkeiten für die Oster-Grenze eine Zahl zuzuordnen, nämlich die Gauß'sche Zahl a. Sie ist das Ergebnis der mathematischen Funktion Modulo. Für a wird die Jahreszahl J durch 19 dividiert und nur mit dem stehen bleibenden Rest weiter gerechnet, was in moderner Schreibweise so lautet:
a = J mod19 (Ergebnis: 0 .. 18) ,
Beispiel 1575: a = 17 ,
Beispiel 2009: a = 14 ,
Beispiel 2014: a = 18 (Ende einer Meton-Periode) .
Der Zahl a entspricht die Goldene Zahl (GZ) der alten Computisten: GZ = a + 1 (Ergebnis: 1 .. 19). Sie mussten derart vorgehen, weil sie noch nicht mit der Null rechnen konnten.
6. Die Berechnung der Oster-Grenze ↑ Anfang
Zu errechnen ist das Datum des Frühlings-Vollmondes als x. März. Sein Abstand vom 21.März habe das Formelzeichen d. Dann ist
x= 21 + d ,
und d kann wieder als ein Modulo-Resultat bestimmt werden.
In einem Jahr mit der Gauß'schen Zahl a = 0 (GZ=1) ist der Frühlings-Vollmond am 36.März (5.April). Die Übereinstimmung mit dem tatsächlichen Vollmond hat der berühmte und für den Beginn der christlichen Jahreszählung (Geburt Christi) verantwortliche Mönch Exiguus z.B. für das Jahr 532 festgestellt.
Für a = 0 muss x=36, also d = 15 sein. Folglich ist
d = ( 15 +19a ) mod30 .
Die auf diese Weise errechenbaren 19 möglichen März(April)tage sind
36(5) / 25 / 44(13) / 33(2) / 22 / 41(10) / 30 /
49(18) / 38(7)
27 / 46(15) / 35(4) / 24 /
43(12) / 32(1) / 21 / 40(9) / 29 / 48 (17)
(Anmerkung 3).
Dass in dieser Gleichung wieder wie schon in a = J mod19 (s.5.) die Zahl 19 vorkommt, ist Zufall. Macht man nämlich die Rechnung rückwärts vom 50. März aus (21+29=50, 19.April als letzte theoretische Oster-Grenze, Anmerkung 4) und rechnet x= 50 - d', dann ist
d' = ( 14 +11a ) mod30 .
Die Summe der beiden Faktoren 19 und 11 ist 30 (ein Bezug zu mod30).
7. Die Berechnung der Sonntags-Distanz ↑ Anfang
Wir wenden uns jetzt unserer zweiten Aufgabe, die weniger leicht als die erste zu lösen ist, zu. Wohlgemerkt, mit dem in Abb.1 erkennbaren Schema ist der Ostersonntag ganz leicht zu finden, aber wir widmen uns den Gauß'schen Osterformeln vielleicht nicht nur aus "akademischen Gründen", sondern auch, weil sie die schnelle Termin-Findung in weit entfernten Jahren ermöglichen.
Zu finden ist der dem Frühlings-Vollmond folgende Sonntag, ausgedrückt als der
y. März. Die zu ermittelnde Distanz e zwischen beiden Ereignissen ist dem Datum x des Frühlings-Vollmondes zu addieren:
y = x + e .
Zu beachten ist, dass der Frühlings-Vollmond immer auf einen anderen Wochentag fällt und die Wochentage (also auch der dem Frühlings-Vollmond folgende Sonntag) jedes Jahr 1 Tag (in Schaltjahren 2 Tage) früher im Kalender steht als im Jahr vorher (Sonntags-Buchstabe im computus). Wir nähern uns der Lösung schrittweise.
<<
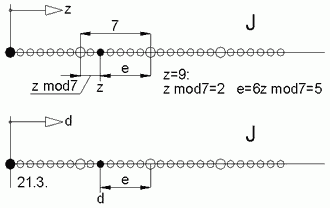Abb.2 Wochentags-Reihe im Jahre J
In Abb.2 sind Kalendertage z eines Jahres J über einige Wochen hinweg aneinander gereiht aufgetragen. Die Reihe beginnt bei z=0 mit einem Sonntag. Die Sonntage sind hervorgehoben dargestellt. Die Zahl der Tage e als Differenz eines Tages bis zum nächsten Sonntag sind als mod7-Rechnung bestimmbar:
Die einfache Rechnung z mod7 liefert bei z-Vergrösserung die ansteigende Reihe
0 , 1 ,..., 5 , 6 , 0 ,... .
Damit liesse sich der Abstand zum vergangenen Sonntag angeben.
Abstand zum nächsten Sonntag ist die absteigende Reihe
0 , 6 , 5 ,..., 1 , 0 , ... , die mit (6z) mod7 gefunden wird:
e = (6z) mod7 .
Zum Vergleich und zur Nachprüfung die beiden Reihen:
z: 0 1 2 3 4 5 6 7 8 9 10
z mod7: 0 1 2 3 4 5 6 0 1 2 3
(6z) mod7: 0 6 5 4 3 2 1 0 6 5 4
Wählt man den 21.März als Nullpunkt auf der Tages-Geraden, er ist in diesem Fall ein Sonntag, so kann z durch d (s.6.) ersetzt werden:
e = (6d) mod7 .
<<
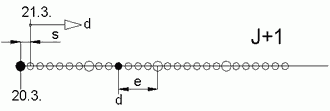Abb.3 Wochentags-Reihe im Jahre J+1
Im Folge-Jahr (J+1) haben aber alle Wochentage ein um 1 (um 2 in Schaltjahren) niedrigeres Datum (Abb.3, vereinfachend ist in dieser und der nächsten Abb. d in unveränderter Grösse dargestellt), bzw. der 21.März ist ein Montag (Dienstag). Die Differenz e wird auch um 1 (2) kleiner, was bei ebenfalls früherem Nullpunkt (20. bzw. 19.März) weiterhin mit mod7 berechenbar ist. Die Nullpunkt-Verschiebung s addiert sich zu d, und es gilt:
e = 6(d+s) mod7 ,
e = (6d + 6s) mod7 {in anderer Schreibweise}.
Nun muss die Verschiebung s als Funktion des Jahres J ermittelt werden.
Die Verschiebung s wird bei Zunahme der Jahre J immer grösser. Schon bald hat der übernächste Sonntag den 21.März passiert. Weil die mod-Rechnung für s das gleiche Ergebnis wie für s'=s+7 (Abb.4) liefert, lässt sich für s auch die gesamte Verschiebung s''=s+7r, die seit Beginn der Christlichen Ära geschehen ist, verwenden:
s = J + (J - J mod4)/4 .
Der erste Summand steht für die jährlichen 1-Tage-Verschiebungen, der zweite für die zusätzlichen 1-Tage-Verschiebungen in den Schaltjahren.
Neben-Ergebnis ist, dass der 21.März im Jahre 0 (1v.Chr.) ein Sonntag war ( s(0)=0 ) .
Wird s in dieser Form in e =(6d + 6s) mod 7 eingesetzt, lassen sich dort zwei mod-Funktionen separieren und dafür kürzer b und c schreiben:
b = J mod4 {s.o.},
c = J mod7 {(J+..) mod7 = (c mod7+..) mod7}.
Damit wird:
e = ( 6d + 6(c+(c-b)/4) mod7 .
Der jetzt in e enthaltene Divisor /4 stört die Eleganz dieses Ausdrucks, die Gauß wie folgt verbesserte [3]:
Die Modulo-Regeln erlauben für mod7 die Addition von 7-fachen Werten im Dividenden, d.h. aus
(c-b)/4 wird (c+7c-b-7b)/4 = 2c-2b,
damit neu für e:
e = ( 6d + 18c - 12b ) mod7 .
Mit erneut erlaubter Addition von -14c und +14b wird:
e = ( 6d + 4c + 2b ) mod7.
Wer wohl ausser Gauß konnte diesen schönen eleganten mathematischen Ausdruck finden? Nur, die damit gelöste Aufgabe ist dieser Gleichung nicht mehr anzusehen .
Eine kleine Korrektur ist noch vorzunehmen:
Die möglichen Werte für e sind 0 ... 6. Im Fall e=0 und d=0 wäre der 21.März Oster-Sonntag, was gemäss Oster-Regelung (s.1.) nicht sein darf. Dieses Rechen-Ergebnis lässt sich vermeiden, wenn d in den Abbildungen 2 bis 4 ab dem 22.März (zuerst ein Montag) gezählt wird. Der gesuchte folgende Sonntag ist dann nicht der 7. sondern der 6.Tag. Die Formel für e ist dann zunächst
e = (6z +6) mod7
und zum Schluss
e = ( 6d + 4c + 2b + 6) mod7 .
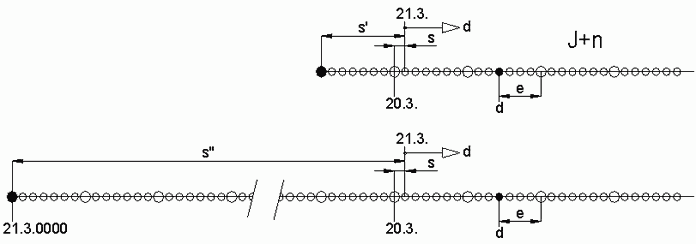Abb.4 Wochentags-Reihe im Jahre J+n (oben) und seit Beginn der Christlichen Ära (unten)
8. Korrekturen durch die Gregorianische Reform:
Sonnen- und Mondangleichung ↑ Anfang
Die Gauß'schen Oster-Formeln in ihrer Sonderform für den Gebrauch im Julianischen Kalender und in ihrer erweiterten Form für den Gregorianischen Kalender werden in 11. einander gegenüber gestellt. Die Unterschiede werden dort diskutiert.
8.1 Oster-Grenze
Im Gregorianischen Kalender wurde - wie allgemein bekannt - ein genauerer Wert für die Jahres-Länge erreicht ( 365,2425 anstatt bisher 365,25 Tage, tatsächlicher Wert 365,2422 Tage), indem 3 von bisher 100 Schalttagen wegfielen.
Für die Korrektur der Oster-Rechnung war zusätzlich nötig, den Fehler in der Meton-Gleichung 19j = 235m = 6.939,75 Tage, die weiterhin als Basis-Beziehung dient, zu berücksichtigen. Mit dem den Reformern bekannten (heute noch gültigen) Wert für die Lunation zu 29,53059 Tagen sind
235 m = 6'939,6887 Tage.
Der Unterschied zu 6.939,75 Tagen beträgt 0,0613 Tage / 19 Jahre oder 1 Tag / ca. 310 Jahre. Der Mond-Monat vergeht schneller als bei Anwendung der Meton-Gleichung berücksichtigt wird.
Die beiden Korrekturen werden als Sonnen- und als Mond(an)gleichung getrennt behandelt [2].
Sonnengleichung:
Das Frühlings-Vollmond-Verteilschema (s.1.: Verfrühung 11 Tage, Verspätung 19/18 Tage) beruht auf 100 Schalt-Tagen in 400 Jahren. Deshalb wird jetzt in jedem der 3 Ausfall-Jahre mit Verfrühung 10 Tage bzw. Verspätung 20/19 Tagen, was allgemein eine Verschiebung gegen später ist, gerechnet.
Mondgleichung:
Um den Fehler in der Meton-Gleichung auszugleichen, gelten bei Anwendung des Schemas alle 310 Jahre die Verfrühung 12 Tage bzw. die Verspätung 18/17 Tage. Die Reform-Kommission erreichte eine Näherung, indem sie dieses Vorgehen für 8 von 25 Säkular-Jahren vorschrieb, erstmals für das Jahr 1800 (dann für die Jahre 2100, 2400, ..., 3900 und 4300). Im Jahr 4300 beginnt der Turnus von vorn.
8.2 Sonntags-Distanz
Durch den Ausfall von Schalt-Tagen wird auch der Verschiebe-Rhythmus der Sonntage gestört.
9. Die korrigierte Oster-Grenze ↑ Anfang
Für die Julianischer Zeit lautet die Oster-Grenze (s.6.):
d = ( 15 +19a ) mod30 .
Der zu findende Korrektur-Wert lässt sich mit der Anfangs-Zahl 15 zusammen als Ausdruck M schreiben:
d = ( M +19a ) mod30 .
M vergrössert sich in jedem Schalt-Ausfalljahr um 1 (Epakte verkleinert), Sonnenangleichung:
M = 15 + (J div100 - J div400 - 2).
Z.B. ist J div100 = J/100, wobei das Ergebnis auf die ganze Zahl abgerundet wird. Diese Art Rechnung heisst Integer-Rechnung mit verschiedenen gebrauchten Schreibweisen, z.B. auch int(J/100) (wir bleiben bei div).
Die Verringerung von M um 2 (-2 in obigem Klammer-Ausdruck) zeigt an, dass vor dem Jahre 300 keine Angleichung erforderlich gewesen wäre, wie man im Rückblick feststellte. Für das Jahr 1600 ist der Klammer-Wert 10, das deckt sich mit den im Jahre der Reform übersprungenen 10 Kalender-Tagen.
Mit
k = J div100 und q = J div400
wird M vorläufig zu:
M = 15 + k - q - 2 .
Wie schon bei den Sonnenangleichungen wurde bestimmt, dass die Mondangleichungen in Säkular-Jahren k stattfinden:
k = J div100 (s.7.) .
M ist innerhalb eines Zeitraumes von 2'500 Jahren 8 mal um je 1 zu verkleinern (Epakte vergrössern). Verlangt ist auch, dass die eine grössere Lücke von 4 in der Reihe von 8 k-Werten diese Periode beendet (Lücke zwischen den Zahlen 2'100 und 2'500).
Der Subtrahend p (für M) in der Form
p = k div25
erhöht sich alle 2'500 Jahre um 1, berücksichtigt somit erst einmal die Perioden-Länge 25 (für k). Nötig sind in diesem Zeitraum 8 Erhöhungen, was durch Multiplikation von k mit 8 erreicht wird:
p = 8k div25
Es entsteht folgende Reihe:
k: 0 * 4 7 10 13 16 19 22 25
p: 0 1 2 3 4 5 6 7 8
Darin ist die Lücke 4 (*) am Anfang anstatt am Ende. Weil die Reformer als Grenzen für die 2'500-Jahr-Periode die Jahre 1800, 4300 usf. bestimmten, gehört die grosse Lücke zwischen die Jahre 1400 und 1800, zwischen 3900 und 4300 usf. Durch Addition von 13 (Anmerkung 5) zu 4k rückt die Lücke 4 tatsächlich zwischen die k-Werte 14 und 18 (Differenz 4).
p = (8k + 13) div25 , mit der Reihe:
k: -1 2 5 8 11 14 * 18 21 24 27 30
p: 0 1 2 3 4 5 6 7 8 9 10
Für das Jahr 500 (p=2) ermittelte man im Rückblick Übereinstimmung zwischen errechneten und astronomischen Mond-Daten, was die Zahl der nötigen Mondangleichungen um 2 verringert. Diese 2 kann gegen die 2 zu Beginn der Christlichen Ära nicht nötigen Sonnenangleichungen verrechnet werden. Beide Zahlen heben sich im Ausdruck für M auf. Für die Zeit der Reform ist p=5, was die damalige Einmal-Korrektur von 3 Tagen bestätigt (5-2=3) [4].
Nach der Zusammenfassung beider Angleichungen ist M endgültig:
M = 15 + k - p - q
Frühlings-Vollmond ist mit verändertem d (verändertem M) der
x.März mit x= 21 + d (s.6.).
10. Die korrigierte Sonntags-Distanz ↑ Anfang
Infolge der in 400 Jahren ausfallenden 3 Schalt-Tage wird das bisher verwendete Muster, nachdem die Sonntage mit den Jahren auf früher fallen (s.7.), auch gestört.
Die Distanz e ist wie M mit dem von der Sonnenangleichung stammenden Ausdruck
+(k - q - 2)zu korrigieren (Zusammenfassung mit +6 ergibt N=k-q+4) :
e = ( 6d + 4c + 2b + N ) mod7.
11. Die Gauß-Formeln für den Julianischen und für den
Gregorianischen Kalender ↑ Anfang
Zusammen gefasst lauten die Gauß'schen Oster-Formeln nun so: