<< Home RekursionInhalt1. Einleitung 1. EinleitungRekursion ist ein in der Natur häufig beobachtbarer und in der Kultur oft nachgestellter Vorgang. Infolge der Anwendung in der Informatik in sogenannten rekursiven Programmen wurde der Begriff Rekursion eigentlich erst in jüngerer Zeit allgemein bekannt. Rekursion ist ein grundsätzlicher natürlicher Vorgang bei der Reproduktion des Lebens, sowohl bei der Erhaltung der Arten als auch beim Wachstum und der Heilung nach Verletzungen von Individuen. Jede Generation von Lebewesen (Tiere und Pflanzen) erzeugt immerzu neue, ihren Individuen mehr oder weniger ähnliche Individuen der nächsten Generation. Bei der Heilung ist der reproduzierende Vorgang - im wesentlichen Zellteilung - immer derselbe. Die Erzeugung neuer Individuen ist hingegen nicht ein streng unveränderlicher Prozess. Es entstehen immer auch gegenüber den Vorgängern mutierte (variierte) Individuen. Diese Eigenschaft ist sowohl typisch bei der variierten Reproduktion des Lebens, als auch bei der verallgemeinerten Beschreibung dessen, was Rekursion ist: "Rekursion ist ... nicht einfache, sondern erweiterte Reproduktion; und Rekursion verschränkt Wiederholung und Variation mit dem Ziel, ein Neues hervorzubringen, ..." [1]. Mit diesem letzen Satz (Zitat) ist der Begrif Rekursion bereits teilweise definiert. Hinzugefügt werden muss - insbesondere bei kulturell nachgestellter Rekursion bzw. bei ihrer Anwendung durch den Menschen, dass die Vorschrift für die erweiterte Reproduktion immer gleich ist, also nur einmal genannt werden muss, und dass im Gegensatz zur Rekursion in der Natur diese nicht unendlich oft und lange vonstatten gehen kann. Automatisierte Rekursion wie in den rekursiven Computerprogrammen verlangt einen dezitierten Eingriff, damit sich der Automat nicht "totläuft". Die eben angedeutete Definition ist noch nicht ausreichend. Die kultuelle Anwendung der Rekursion ist sehr vielseitig. Sie wird in den verschiedenen Anwendungsgebieten nie alle anderen Gebiete einschließend dargestellt bzw. definiert. Ich werde auch keinen, vermutlich nicht gelingenden Versuch, eine alle Gebiete einschließende allgemeine Definition zu finden, anstellen. Dafür werde ich eine größere Zahl von Anwendungsbeispielen besprechen. 2. Sprache, Musik, RundfunkreportageDas Vorkommen der Rekursion in der Sprache ist eigentlich noch kein typisches Anwendungsbeispiel, weil Sprechen zur Natur des Menschen gehört. Rekursion dabei ist, dass ein gesprochener Satz einen Nebensatz enthalten kann, der Nebensatz wieder einen Nebensatz enthalten kann, ... und so fort. Das zeigt einerseits den prinzipiell unnendlichen Vorgang Rekursion und andererseits, dass die Teilvorgänge und die Teilergebnisse einander ähnlich und aufeinander bezogen sind. Die Regeln für die Satz- und Nebensatzbildung sind gleich. In Realität wird die Unendlichkeit vermieden, weil dem Sprechenden bald einmal die Luft aus- und ihm und dem Hörer der Faden verloren-geht. In der Linguistik wird Rekursion als ein Begriff angesehen, "der die formale Eigenschaft von Grammatiken bezeichnet, mit einem endlichen Inventar von Elementen und einer endlichen Menge von Regeln eine unendliche Menge von Sätzen zu erzeugen" [2]. Das gilt vor allem für das Schreiben von Sätzen, womit jetzt ein typisches Anwendungsbeispiel gefunden ist. Aber auch hierbei bleibt es aus den o.g. Gründen bei nicht allzu langen Sätzen [3]. Dass Rekursion außer in der Sprache auch in der Musik vorkommt, ist naheliegend, denn: "Rekursive ... Strukturen sind in drei kognitiven Domänen grundlegend, in denen der Mensch besondere Fähigkeiten aufweist: der Sprache, der Musik und der Mathematik." [4] Bei der Musik wird oft von der Verschachtelung, die ein weiteres Merkmal von Rekursion ist, gesprochen. Wie die gesprochenen Nebensätze in Nebensätzen und Hauptsatz, sind z.B. auch in verschiedenen Tonarten gehaltene Themen einer Sonate ineinander verschachtelt. Hierbei verläuft der verschachtelte Vorgang Rekursion nicht wie im Allgemeinen überwiegend voran, sondern als Reprise zurück zum Anfang. Ein ähnlicher, rückführender verschachtelter Vorgang ist in den Nachrichtensendungen im Fernsehen und im Radio zu beobachten: Der Sprecher schaltet zu einen Reporter vor Ort des Geschehens um. Dieser lässt eine Person, die das Geschehen direkt beobachtet hat, ins Mikrofon sprechen. Der Vorgang kann auf verschiedenene Stufen hin- und hergehen, endet aber schließlich wieder im Studio beim Nachrichtensprecher [5]. Prizipiell ins Unendliche führendes Vorangehen findet in beiden Fällen nicht statt, dennoch wird von Rekursion, die ja auf Deutsch auch nur zurückkehren bedeutet, gesprochen. Bevor ich mich der Mathematik, der dritten besonderen kognitiven Fähigkeit des Menschen und der darin vorkommenden Rekursion zuwende, behandle ich noch ein paar "Alltags"-Anwendungen von Rekursion. 3. Puppe in der Puppe
Die in Abb.1 gezeigte russische Matrjoschka besteht aus fünf ineinander steckbaren Puppen. 4. Zwischen zwei parallelen Spiegeln
Die Bilderreihe zwischen zwei, Spiegeln ist nahe verwandt mit den natürlichen Rekursions-Vorgängen. Kultureller Beitrag ist lediglich, zwei Spiegel parallel zueinander anzuordnen. Die Rekursion braucht nicht angestoßen zu werden; sie ist zwischen den einander zugekehrten Spiegeln permanent "in Betrieb". Ein zwischen den Spiegeln angebrachter Gegenstand spiegelt sich in beiden Spiegeln. Da sich jeder der beiden Spiegel im anderen spiegelt, werden auch die in den Spiegeln vorhandenen virtuellen Bilder im jeweils anderen Spiegel mit gespiegelt. Das die Bilder erzeugende Licht läuft endlos zwischen den Spiegeln hin und her, was einen endlosen rekursiven Vorgang darstellt. Weil die Bildweite mit der Zahl der Spiegelungen zunimmt, wird der Bildwinkel zunehmend kleiner. Diese Änderung ist das Rekursions-Merkmal erweiterte Reproduktion. Die Bilder werden nicht nur immer kleiner und deshalb nicht mehr erkennbar, sondern sie werden auch schwächer, weil das Licht beim Lauf durch die Luft und bei jeder Reflexion an Stärke verliert. Aber auch ohne das gäbe es ein natürliches Ende, indem es keine Bilder, die kleiner als die Wellenlänge des Lichts sind, geben kann. Den Eindruck, den man zwischen zwei parallelen Spiegeln sitzend erfährt, hat der Berner Mundartdichter und -sänger Mani Matter in einem Lied geschildert [6]. Er saß vor einem Spiegel beim Friseur, wo es einen zweiten Spiegel hinter dem Kunden gab. Matter erwähnt, dass er seinen Kopf auch von hinten - also beide Bildreihen - sah, was darauf hindeudet, dass die Spiegel nicht besonders genau parallel waren. In Abb.2 ist die Parallelität besser, denn die Foto-Kamera sieht sich nicht von hinten. Nur die Rückseite der seitlich befindlichen Person sieht sie teilweise noch; die Person selbst wird sich nur von vorne sehen. 5. Rad des Theodorus, Pythagoras-Baum, fraktale MusterMeine ersten Rekursions-Beispiele aus der Mathematik sind rekursive Zusammenhänge, die sichtbar sind, also Graphiken.
Zuerst sei das Rad des im 5. Jahrhundert v.Chr. lebenden griechischen Mathematikers Theodorus, das überhaupt für das erste Beispiel für die - vermutlich noch unbewusste - Beschäftigung des Menschen mit Rekursion gehalten wird, besprochen (Abb.3). Es wird auch Wurzelschnecke genannt, weil Theodorus damit die Irrationalität der Wurzelwerte der Zahlen 3 bis 17 bewiesen haben soll (der Beweis für Wurzel aus 2 sei schon bekannt gewesen). Die rekursive Bildungsregel ist:
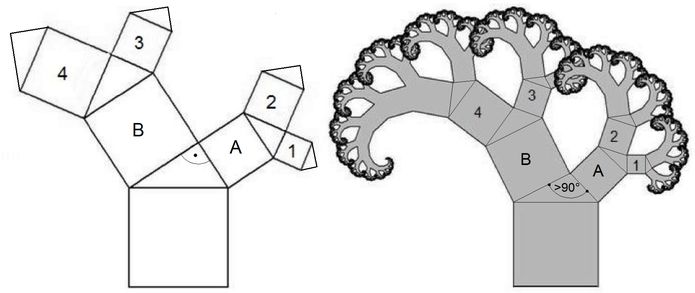
Beim sogenannten Pythagoras-Baum (Abb.4) wird von einem unter der Hypotenuse eines rechtwinkligen Dreiecks gezeichneten Quadrat ausgegangen. Daher der Name, obwohl die Rechtwinkligkeit im Dreieck keine Voraussetzung für das Gewinnen einer solchen Baumstruktur ist (siehe Abb.4, rechts). Rekursiv erzeugte Graphiken wie der Pythagoras-Baum können seit der Prägung des mathematischen Begriffs Fraktal (Benoît Mandelbrot, 1975) als fraktale Muster bezeichnet werden. Gleichzeitig mit dem Erscheinen des Begriffs Fraktal wendeten sich auch vermehrt Künstler rekursiv erstellbaren Graphiken zu, z.B. Karl Gerstner (Abb.5). Er und viele andere Künstler wurden dazu direkt durch die Darstellung der Mandelbrot-Menge ("Apfelmännchen") angeregt. So wie dort die Ränder der schwarzen Flächen durch immer kleinere Strukturn dargestellt sind, bestehen die Ränder des äußeren und der größeren inneren Kreise aus nach rekursivem Bildungsgesetz entstandenen, immer kleiner werdenden Kreisen. Das Füllen der Lücken zwischen diesen Kreisen und zwischen ihnen und den gedachten Rändern mit ebenfalls Kreisen verschiedener Größe ist möglicherweise ein gesonderter rekursiver Vorgang.
6. Mathematik: rekursive Definition
Diese in der Mathematik gebrauchte Wortkombination ist in zweifacher Hinsicht verwirrend: Ich persönlich fasse den Begriff Definition enger auf: ein Sachverhalt wird verbindlich in einer bestimmten Weise benannt. Für das, was hier und auch anderenorts oft gemeint ist, verwende ich lediglich beschreiben mithilfe von erkannten Zusammenhängen, gewissermassen unverbindlich beschreiben, oder einfach auch nur erklären.
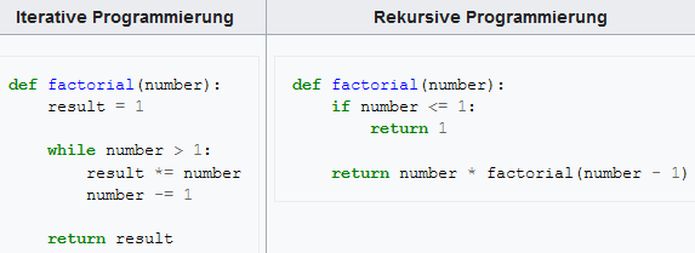
7. Rechner-ProgrammierungDie o.g. Beispiele aus der Mathematik sind zu leicht, um sie für sogenanntes rekursives Programmieren zu benutzen, sie sind dafür sogar ungeeignet: "Tatsächlich hat die Erklärung des Konzeptes rekursiver Algorithmen anhand von ungeeigneten Beispielen wesentlich zur Entstehung einer weitverbreiteten Abneigung und Antipathie gegen die Rekursion in der Programmierung beigetragen und zur Gleichsetzung von Rekursion mit Ineffizienz geführt." [9a] Rekursive Programme benötigen nämlich mehr Speichervolumen im Rechner als konventionelle, sogenannte iterativ formulierte Programme und sind auch bereits in solchen einfachen Ausführungen schwerer zu verstehen. "Rekursive Algorithmen eigenen sich besonders, wenn das zugrundeliegende Problem .... rekursiv definiert" [9a] ist. Die rekursive Definition in den genannten Beispielen existiert nicht à priori, sondern sie ist das Ergebnis mathematischer Übungen. Es "bedeutet nicht, dass eine ... rekursive Definition eine Garantie dafür bietet, dass ein rekursiver Algorithnus der beste Weg zur Lösung des Problems ist." [9a] Nikolaus Wirth "zeigt die Entwicklung rekursiver Programme in Fällen, in denen Rekursion angebracht ist", zahlreich auf über 50 Seiten seines Buches [9b]. Die dabei gelösten Probleme sind alle recht anspruchsvoll, so dass hier ncht darauf eingegangen werden kann. Lediglich erwähnt sei das Problem der acht Damen [9c], das C.F. Gauss 1850 untersuchte. Es war analytisch nicht vollständig lösbar. Die Lösung gelang erst mithilfe der heutigen automatischen Rechner. Dafür, dass auf einen Schachbrett acht Damen so aufgestellt sind, dass sie sich nicht gegenseitig bedrohen, gibt es 12 signifikant verschiedene, nicht symmetrische Lösungen. Das in Pascal geschriebene Programm nimmt nicht einmal 1 Seite des Buches ein [9d]. Es verlockt dazu, es gelegentlich einmal austzprobieren. Zum Programm-Code ist anzumerken, dass es den sogenannten Selbstaufruf damals, als die 3. Auflage des Buches erschien, noch nicht gab. Umgeschrieben darauf sind die von Wirth angegebenen rekursiven Programme etwas kürzer. In Abb.7, rechts ist ein unter Verwendung eines Selbstaufrufes einer Funktion verfasstes rekursives Programm gezeigt.
Niklaus Wirth ist ein bedeutender Vordenker für Rechner-Programmmierung. Zudem hat er mehrere Programmiersprachen (z.B. Pascal) geschaffen, deshalb zum Abschluss noch zwei Zitate aus seinem Buch [9]: 8. Quellen-Verzeichnis
[1] Hartmut Winkler: Über Rekursion, Teil 1, letzter Absatz
|
Abb.2 Rekursive Bilderreihe wischen zwei Spiegeln in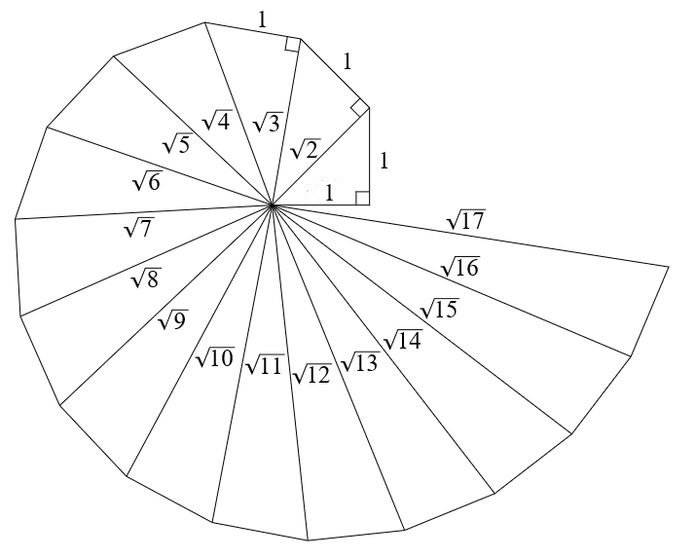
Abb.3 Rad des Theodorus mit rekursiver Bildungsregel
