|
<< Home Planetengetriebe am FahrradDer allgemeindere Begriff ist Umlaufrädergetriebe anstatt Planetengetriebe. Inhalt1. Einleitung2. Das Planetengetriebe 3. Planetengetriebe in Nabenschaltungen 4. Planetengetriebe in elektrischen Nabenmotoren 5. Planetengetriebe in der Hinterradnabe des Elektro-Fahrrades Swissbee® 1. Einleitung ↑ AnfangAm Fahrrad kommt das einfache, mit einem Hohlrad versehene Zahnrad-Planetengetriebe in drei mir bekannten Anwendungen vor:
Es dient wie jedes Getriebe vorwiegend zur Umformung von Drehzahlen und Drehmomenten. In der Hinterradnabe des Swissbee® ist es zudem ein Additionsgetriebe. Die beiden eingehenden, vom Pedal- und vom Elektroantrieb stammenden Drehungen und Drehmomente werden addiert und als Drehung des Hinterrads und als das an ihm wirksame Drehmoment abgegeben. 2. Das Planetengetriebe ↑ AnfangAbb.1 zeigt den prinzipiellen Aufbau des zu besprechenden Planetengetriebes. Das zentrale Zahnrad (Sonnenrad, grau) wird von mehreren Zahnrädern (Planetenrädern, blau) umkreist. Diese sind auf dem gemeinsamen Planetenträger (oder Steg, ebenfalls blau) drehbar gelagert. Konzentrisch zum Sonnenrad drehen sich Steg und äußeres Hohlzahnrad (rot). Durch die konzentrische Anordnung dieser drei drehbaren Teile ist das Getriebe für den Einsatz in einer Radnabe prädestiniert. Zudem besteht es aus relativ wenig Rädern (grundsätzlich wäre mir nur einem Planetenrad auszukommen).
aus zentralem Sonnenrad (grau), mehreren Planetenrädern (blau) auf gemeinsamen Planetenträger (Steg, blau) und umfassenden Hohlrad (rot) [www.buk-online.de] In allgemeiner Getriebe-Anwendung ist eins der drei Hauptteile festgehalten (fixiert). Das zweite Teil ist getrieben (Antrieb) und treibt seinerseits das dritte Teil (Abtrieb). Bei zum Beispiel fixiertem Sonnenrad findet vom Steg zum Hohlrad eine Übersetzung ins Schnelle statt. Vom Hohlrad zum Steg wird ins Langsame untersetzt. (Die technisch korrekte Sprachregelung ist dem entgegengesetzt: Übersetzung kleiner als Eins bzw. Übersetzung größer als Eins.) Wenn sich alle drei Wellen drehen können, muss ein zweiter Antrieb oder ein zweiter Abtrieb vorhanden sein, damit die Bewegungsverhältnisse eindeutig sind (Fachausdruck: damit Zwanglauf herrscht). Bei zwei Antrieben spricht man von einem Additions-Getriebe, bei zwei Abtrieben von einem Verzweigungsgetriebe. Der erste Fall liegt z.B. beim Swissbee® vor.
Abb.2 Schema eines Automobil-Diferentialgetriebes Ein Verzweigungsgetriebe ist das vom Automobil bekannte Differentialgetriebe. Es verzweigt den Antrieb auf zwei Räder. Weil diese beiden Räder im Normalbetrieb (Geradeausfahrt) gleich schnell drehen müssen, ist das Differentialgetriebe von symmetrischer Bauart. In der Ausführung mit Kegelrädern geht die Anlalogie der Räder mit einer Sonne und sie umkreisenden Planeten verloren. Geblieben sind die umlaufenden Achsen mit den darauf drehenden Rädern (in Abb.2 nur eine Achse und nur ein Rad, grün), was im gegenüber Planetenrädergetriebe (kürzer: Planetengetriebe) allgemeineren Fachbegriff Umlaufrädergetriebe zum Ausdruck kommt. 3. Planetengetriebe in Nabenschaltungen ↑ Anfang
In der klassischen Nabenschaltung wird das Hohlrad-Planetengetriebe zur Erzeugung von drei Getriebestufen verwendet. Eine solche Schaltung wurde um 1900 von Sturmey-Archer auf den Markt gebracht. Seit den zwanziger Jahren gibt es auch die bekannte Torpedo®-Dreigangschaltung von Fichtel und Sachs. Der jeweilige mittlere Gang ist direkt, An- und Abtrieb werden unmittelbar miteinander gekoppelt (2. Gang), das Getriebe wird umgangen. Beim Antrieb des Hohlrades dreht der mit der Nabe gekoppelte Steg langsamer (1. Gang). Wird der Antrieb mit dem Steg und das Hohlrad mit der Nabe gekoppelt, liegt der schnellere 3. Gang vor. Das Sonnenrad ist immer fix, es ist fester Bestandteil der fix ins Fahrrad eingebaute Nabenachse. Die Dreigang-Nabenschaltungen der beiden genannten und weiterer Hersteller waren und sind patentiert. Das Grundprinzip unter Verwendung eines Hohlrad-Planetengetriebes ist inzwischen Stand der Technik geworden, die Patentansprüche beziehen sich auf die übrigen Elemente, vor allem auf die Mittel zur schaltbaren Kopplung.
In einer ausgeführten Dreigang-Nabenschaltung (Abb.4, vermutlich Torpedo®) nehmen die schaltbaren Koppelelemente mehr Platz als das Planetengetriebe ein. Das wichtigste Teil ist die schraffiert dargestellte Schiebemuffe. Sie wird mit Federkraft an der vorgewählten Stelle auf der Nabenachse gehalten. Über ihren rechten Koppelzahnkranz und einer nicht verschieblichen Hülse mit entsprechendem Hohl-Koppelzahnkranz ist sie ständig zur Drehmomentübertragung mit dem Ketten-Zahnritzel (rechst außen) verbunden. Ihr linker Koppelzahnkranz greift in einen entsprechenden Hohl-Koppelzahnkranz am Holzahnrad (1. und 2. Gang) oder am Steg (3. Gang) ein. Die Kopplung mit der Nabe erfolgt mit Freilaufgesperren, im 1. Gang vom Steg zur Nabe (links und Ansicht A) im 2. und 3. Gang vom Hohlzahnrad (rechts) zur Nabe. Weil das Hohlzahnrad immer schneller dreht als der Steg, muss im 1. Gang das sich am Hohlzahnrad befindliche Gesperre außer Betrieb gesetzt werden. Dafür wird das Hohlzahnrad ein kleines Stück nach rechts verschoben. Im 2. und 3. Gang ist das andere Gesperre in Freilauffunktion. Die Drehzahl des Kettenzahnritzels kann in jedem Gang kleiner als die der Nabe sein, das heisst, dass diese Nabenschaltung auch nach außen Freilauffunktion hat, dass sie eine Nabe mit Freilauf ist. Der Kutzbach-PlanBei Getrieben mit umlaufenden Achsen sind die Geschwindigkeits- und Drehzahlverhältnisse weniger leicht zu überblicken als bei Standgetrieben. Hierbei bedient man sich mit Vorteil einer graphischen Methode, die Karl Kutzbach am Anfang des vorigen Jahrhunderts an der Technischen Hochschule in Dresden erarbeitete.
Abb.5 Kutzbachplan für das Hohlrad-Plantengetriebe von Abb.4 (fixiertes Sonnenrad) Den Kutzbachplan für das Hohlrad-Plantengetriebe aus Abb.4 (fixiertes Sonnenrad) zeigt Abb.5. Die vertikale Achse ist die Räderachse, auf der die Lage und die Radien der Zahnäder enthalten sind. Auf der horizontalen Achse ist die Umfangsgeschwindigkeit als radiale Funktion jedes Rades ablesbar. Primär interessieren die Umgangsgeschwindigkeiten der Wälzkreise der Räder. Das bis hier her erklärte Diagramm ist der sogenannte Geschwindigkeitsplan. Für den sogenannten Drehzahlplan lässt man alle Geschwindigkeitsgeraden von einem gemeinsamen Punkt ausgehen und mit einer zu den Achsen parallelen Geraden (Drehzahlgerade) schneiden. Der Drehzahlplan in Abb.5 wäre komplett, wenn man parallel zur Geschwindigkeitsgerade der Planetenräder eine Gerade durch den Nullpunkt des Geschwindigkeitsplans zusätzlich zeichnen würde. Deren Schnittpunkt mit der Drehzahlgeraden würde dort ihre zu den beiden anderen Drehzahlen relativ hohe Drehzahl anzeigen.
Aus Abb.5 ist ablesbar (Indizes: Ri für Kettenzahnritzel, Na für Nabe): Dazu passende Zähnezahlen wären 25 für das Sonnenrad und 17 für die Planetenräder (59 für das Hohlrad). Gemäß Quellentext sind es 17 und 15 (die Skizze ist in der Quelle nicht massstäblich und zudem verzerrt), was etwa die Werte 1,36 und 0,73 ergibt, und der größere Wert ist 185% des kleineren. Klassische Fünfgang-NabeDie Planetenrad-Nabenschaltungen mit mehr als 3 Gängen sind Erweiterungen des bisher besprochenen Planetengetriebes. Sie sind in der Regel nicht einfache Reihenschaltungen des Grundtyps, sondern mehrere davon sind ineinanander verwoben. Als Beispiel sei das Fünfganggetriebe genannt, das bei Sturmey-Archer und bei Fichtel und Sachs auf dem gleichen Grundschema beruht (Abb.6).
Abb.6 Klassische Fünfgang-Nabe Vom zweiten Grundtyp fehlen das Hohlrad und der Steg. Das Sonnenrad und die Planetenräder sind doppelt vorhanden, beide haben aber unterschiedliche Abmessungen. Die unterschiedlichen Planetenräder sitzen paarweise und untereinander fix auf dem Steg, nur die kleineren Räder kämmen mit dem Hohlrad. Andererseits kämmen die kleineren Planetenräder mit dem größeren Sonnenrad und die größeren Planetenräder mit dem kleineren Sonnenrad. Eines der beiden Sonnenräder wird fixiert, das andere bleibt drehbar. Bei fixiertem großen Sonnenrad wird die größte und die kleinste Übersetzung erreicht (1. und 5. Gang, Hohlrad bzw. Steg treibend). Wenn das kleine Sonnenrad fix ist, entstehen zwei Zwischen-Gänge (2. und 4. Gang, Hohlrad bzw. Steg treibend). Der 3. Gang ist wie bisher die direkte Kopplung zwischen An- und Abtrieb.
Aus Abb.6 ist ablesbar (Indizes: Ri für Kettenzahnritzel, Na für Nabe, 1 für großes Sonnenrad, 2 für kleines Sonnenrad): 4. Planetengetriebe in elektrischen Nabenmotoren ↑ AnfangIn dieser Anwendung wird i.d.R. ebenfalls von einem Planetengetriebe gesprochen, obwohl die auf einem Kreis angeordneten Zwischenräder nicht umlaufen, sondern sich nur drehen. Die Achse der Nabe (und die Achsen der Zwischenräder) sind der ruhende Teil. Ein mit ihr koaxial eingebauter Elektromotor ist vorteilhaft ein Außenläufer: Sein Stator befindet sich innen und umschließt die Nabenachse. Die jeden Elektromotor kennzeichnenden Polpaare haben im einfachen Fall nur einen Spulen-Magnet, der andere ist ein Permanent-Magnet, so auch beim Motor im Elektro-Fahrrad. Um den Motorstrom nicht über Schleifkontakte führen zu müssen, sind die Spulen-Magnete Teil des Stators, die Permanent-Magnete sitzen auf dem Außenläufer-Rotor (Abb.7).
Damit das von einem Elektromotor abgegebene Drehmoment (und damit die Leistung) einen optimalen Wert hat, muss seine Drehzahl einen Mindestwerrt haben. Die passende Drehzahl verringert sich, wenn der Motor mehr als ein Polpaar hat. Es gibt Nabenmotoren mit bis zu 40 Polpaaren, die für kleine Fahrrad-Laufräder gut geeignet sind. Für die meist verwendeten 28-Zoll-Laufräder ist aber deren Drehzahl noch zu hoch, weshalb ein ins Langsame übersetzendes Getriebe nachgeschaltet wird (anstatt den Motor mit weiteren Polpaaren zu versehen und ihn dadurch unverhältnismässig groß und schwer zu machen). Ein solches Getriebe ähnelt dem aus den Nabenschaltungen gut bekannten Planetengetriebe mit Hohlrad (Abb.8).
5. Planetengetriebe in der Hinterradnabe des Elektro-Fahrrades Swissbee® ↑ AnfangIn der Hinterradnabe des Elektro-Fahrrades Swissbee® wird das Planetegetriebe mit Hohlrad als Additionsgetriebe verwendet (Abb.9). Am Laufrad (Mitte: Scheibenrad und Welle als Steg, blau) addieren sich die Drehzahlen des Fahrers (rechts: Kettenritzel auf dem Hohlrad, rot) und des Elektromotors (links: Zahnriemenscheibe auf dem Sonnenrad, magenta). Das Swissbee® hat somit ein prinzipiell anderes Antriebskonzept als alle anderen Fahrräder mit elektrischem Zusatzantrieb. Es ist allgemein üblich, dass die Drehzahlen des Fahrer- und des Motorantriebs voneinander unabhängig sind, beziehungsweise, dass beide das Hinterrad (oder Hinter- und Vorderrad bei Zweiradantrieb) gleich schnell antreiben. Dabei braucht das von beiden am Laufrad stammende Dehmoment nicht gleich zu sein. In die Swissbee®-Nabe hingegen ist das Verhältnis der antreibenden Drehmomente unveränderlich nach Festlegung der Zahnradgrößen eingebaut. Bei gleich großen Sonnenrad und Planetenrädern ist der wirksame Hebelarm des Kettenradantriebs dreimal größer als der des Elektroantriebs (Wälzkreisdurchmesser des Hohlrades zu dem des Sonnenrades).
Im Kutzbachplan (Abb.10) sind mehrere Drehzahl-Summen dargestellt. Teilbild a zeigt den allgemeinen Fall. Teilbilder b und c stellen die Grenzfälle dar:
<< andere Fahrrad-Beiträge |

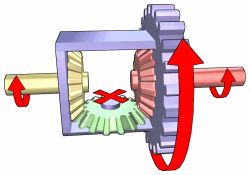
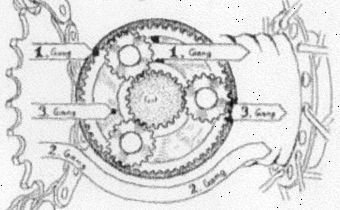 Abb.3 Dreigang-Nabenschaltung mit Hohlrad-Planetengetriebe, Sonnenrad fix auf der Radachse
Abb.3 Dreigang-Nabenschaltung mit Hohlrad-Planetengetriebe, Sonnenrad fix auf der Radachse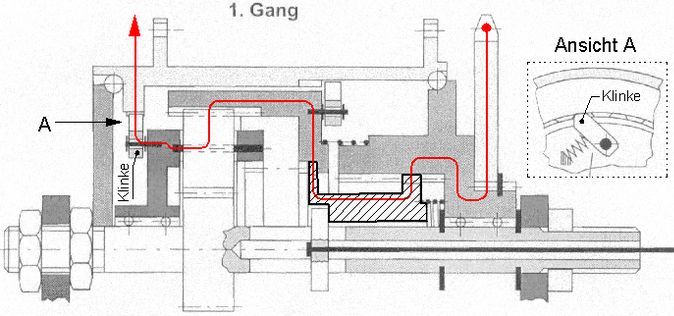
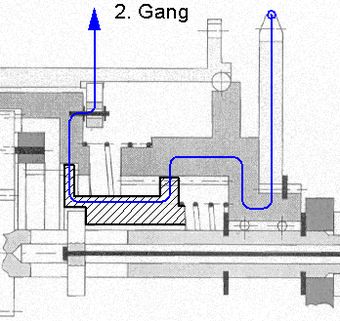
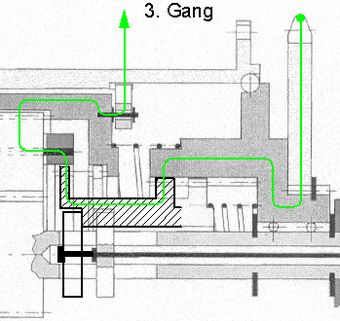 Abb.4 Dreigang-Nabenschaltung, schematisch, [
Abb.4 Dreigang-Nabenschaltung, schematisch, [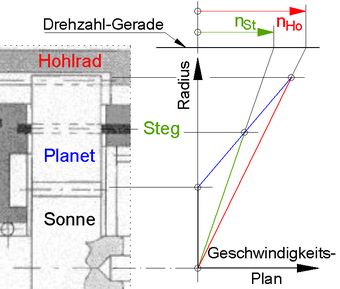
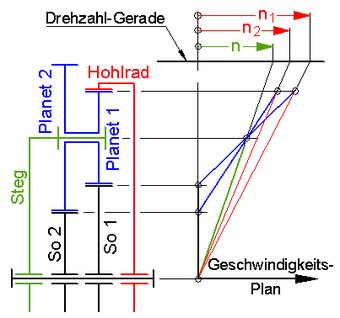
 Abb.7 Nabenmotor mit Außenläufer
Abb.7 Nabenmotor mit Außenläufer 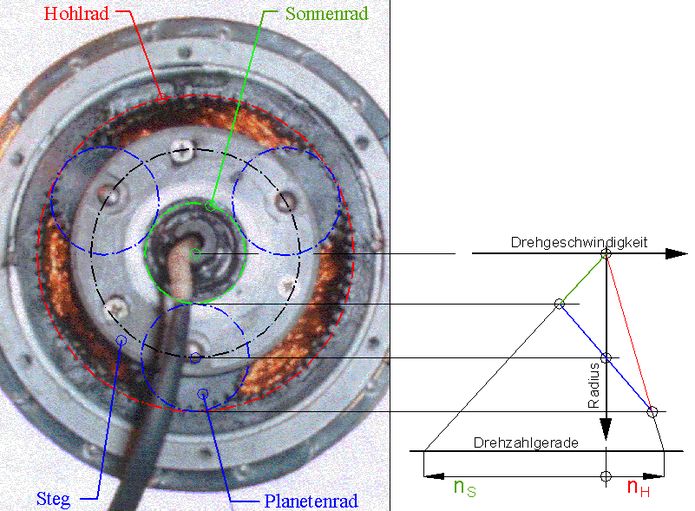 Abb.8 Nabenmotor mit Untersetzungsgetriebe
Abb.8 Nabenmotor mit Untersetzungsgetriebe 
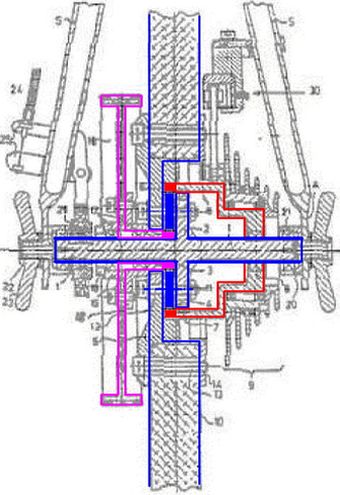 Abb.9 Hinterradnabe des Elektro-Fahrrades Swissbee® rechtes Bild: Patentschrift-Zeichnung, Getriebe nachgefärbt
Abb.9 Hinterradnabe des Elektro-Fahrrades Swissbee® rechtes Bild: Patentschrift-Zeichnung, Getriebe nachgefärbt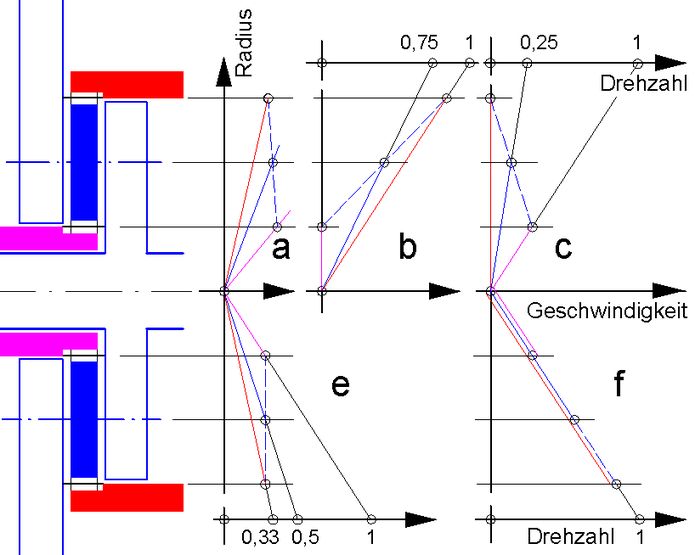 Abb.10 Kutzbachplan für das Hohlrad-Plantengetriebe von Abb.9 (3 koaxial drehende Teile, gleiche Wälzkreisdurchmesser für Sonnenrad und Planetenräder)
Abb.10 Kutzbachplan für das Hohlrad-Plantengetriebe von Abb.9 (3 koaxial drehende Teile, gleiche Wälzkreisdurchmesser für Sonnenrad und Planetenräder)